题目内容
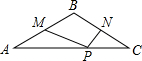 如图在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是________.
如图在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是________.
4+2
分析:首先要明确P点在何处,作点M关于AC的对称点M′,根据勾股定理求出MN的长,由三角形中位线的性质及三角函数分别求出AB、BC、AC的长,从而得到△ABC的周长.
解答:作M点关于AC的对称点M′,连接M'N,与AC的交点即是P点的位置,
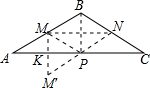 ∵M,N分别是AB,BC的中点,
∵M,N分别是AB,BC的中点,
∴MN是△ABC的中位线,
∴MN∥AC,MN= AC,
AC,
∴ =
= =1,
=1,
∴PM′=PN,
∴MP=PN,
∵在△MBP和△NBP中,
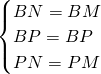 ,
,
∴△MBP≌△NBP(SSS),
∴∠ABP=∠CBP=60°,
∵AB=BC,
∴AP=PC,
即:当PM+PN最小时P在AC的中点,
∵PM+PN的最小值为2,
∴PM=PN=1,MN= ,
,
∴AC=2 ,
,
AB=BC=2PM=2PN=2,
∴△ABC的周长为:2+2+2 =4+2
=4+2 .
.
故答案为: .
.
点评:本题考查等腰三角形的性质和轴对称最短路线,及三角函数等知识的综合应用.正确确定P点的位置是解题的关键.

分析:首先要明确P点在何处,作点M关于AC的对称点M′,根据勾股定理求出MN的长,由三角形中位线的性质及三角函数分别求出AB、BC、AC的长,从而得到△ABC的周长.
解答:作M点关于AC的对称点M′,连接M'N,与AC的交点即是P点的位置,
 ∵M,N分别是AB,BC的中点,
∵M,N分别是AB,BC的中点,∴MN是△ABC的中位线,
∴MN∥AC,MN=
 AC,
AC,∴
 =
= =1,
=1,∴PM′=PN,
∴MP=PN,
∵在△MBP和△NBP中,
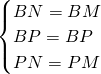 ,
,∴△MBP≌△NBP(SSS),
∴∠ABP=∠CBP=60°,
∵AB=BC,
∴AP=PC,
即:当PM+PN最小时P在AC的中点,
∵PM+PN的最小值为2,
∴PM=PN=1,MN=
 ,
,∴AC=2
 ,
,AB=BC=2PM=2PN=2,
∴△ABC的周长为:2+2+2
 =4+2
=4+2 .
.故答案为:
 .
.点评:本题考查等腰三角形的性质和轴对称最短路线,及三角函数等知识的综合应用.正确确定P点的位置是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
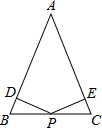
 已知,如图在等腰三角形ABC中,AB=AC,P为BC的中点,PD⊥AB于点D,PE⊥AC于点E,求证:PD=PE.
已知,如图在等腰三角形ABC中,AB=AC,P为BC的中点,PD⊥AB于点D,PE⊥AC于点E,求证:PD=PE. 12、如图,等腰三角形ABC中,P为底边BC上任意点,过P作两腰的平行线分别与AB,AC相交于Q,R两点,又P′是P关于直线RQ的对称点,证明:P′在△ABC的外接圆上.
12、如图,等腰三角形ABC中,P为底边BC上任意点,过P作两腰的平行线分别与AB,AC相交于Q,R两点,又P′是P关于直线RQ的对称点,证明:P′在△ABC的外接圆上. 已知,如图在等腰三角形ABC中,AB=AC,P为BC的中点,PD⊥AB于点D,PE⊥AC于点E,求证:PD=PE.
已知,如图在等腰三角形ABC中,AB=AC,P为BC的中点,PD⊥AB于点D,PE⊥AC于点E,求证:PD=PE.