题目内容
 12、如图,等腰三角形ABC中,P为底边BC上任意点,过P作两腰的平行线分别与AB,AC相交于Q,R两点,又P′是P关于直线RQ的对称点,证明:P′在△ABC的外接圆上.
12、如图,等腰三角形ABC中,P为底边BC上任意点,过P作两腰的平行线分别与AB,AC相交于Q,R两点,又P′是P关于直线RQ的对称点,证明:P′在△ABC的外接圆上.分析:①容易得到三角形AP'Q全等于PRQ,所以∠P'AQ=∠QRP;
②由对称关系得到,∠QRP=∠QRP',所以∠QRP'=∠P'AQ,所以P',A,R,Q四点共圆,进一步可以得到∠AP'B+∠BCA=180度,所以ABCP'四点共圆,P′在△ABC的外接圆上.
②由对称关系得到,∠QRP=∠QRP',所以∠QRP'=∠P'AQ,所以P',A,R,Q四点共圆,进一步可以得到∠AP'B+∠BCA=180度,所以ABCP'四点共圆,P′在△ABC的外接圆上.
解答: 证明:连接P'Q,P'A,QR,
证明:连接P'Q,P'A,QR,
∵QP∥AC,PR∥AB
∴四边形ARPQ为平行四边形
∴AQ=PR
P′Q=PQ
∠RQP=∠P′QA
∴△AP′Q≌△PRQ
∴∠P'AQ=∠QRP;
由对称关系得到,∠QRP=∠QRP',所以∠QRP'=∠P'AQ,所以P',A,R,Q四点共圆,
∴∠QP'R=∠BAC
同理得到∠QBP'=∠QP'B,∠RP'A=∠BAP'
∴可以得到∠AP'B+∠BCA=180度,所以ABCP'四点共圆,
∴P′在△ABC的外接圆上.
 证明:连接P'Q,P'A,QR,
证明:连接P'Q,P'A,QR,∵QP∥AC,PR∥AB
∴四边形ARPQ为平行四边形
∴AQ=PR
P′Q=PQ
∠RQP=∠P′QA
∴△AP′Q≌△PRQ
∴∠P'AQ=∠QRP;
由对称关系得到,∠QRP=∠QRP',所以∠QRP'=∠P'AQ,所以P',A,R,Q四点共圆,
∴∠QP'R=∠BAC
同理得到∠QBP'=∠QP'B,∠RP'A=∠BAP'
∴可以得到∠AP'B+∠BCA=180度,所以ABCP'四点共圆,
∴P′在△ABC的外接圆上.
点评:此题主要考查了四点共圆,点的对称性,三角形的全等证明,综合性较强.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
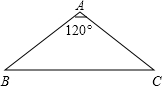 如图,等腰三角形ABC的顶角为120°,底边BC=
如图,等腰三角形ABC的顶角为120°,底边BC=
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
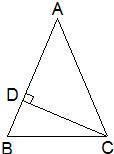 9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( )
9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( )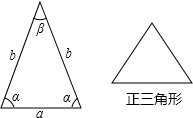 (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?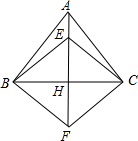 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,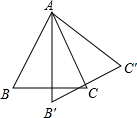 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转