Question

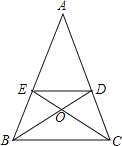
【题目】如图，△ABC是等边三角形，AB＝6，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一动点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．

（1）证明：在运动过程中，点D是线段PQ的中点；

（2）当∠BQD＝30°时，求AP的长；

（3）在运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

Answer 1

【答案】（1）见解析；（2）AP＝2；（3）DE的长不变，定值为3．

【解析】

（1）过P作PF∥QC交AB于F，则是等边三角形，根据AAS证明三角形全等即可；

（2）想办法证明BD＝DF＝AF即可解决问题；

（3）想办法证明即可解决问题．

（1）证明：过P作PF∥QC交AB于F，则是等边三角形，

∵P、Q同时出发，速度相同，即BQ＝AP，

∴BQ＝PF，

在和中，

，

∴，

∴DQ＝DP；

（2）解：∵，

∴BD＝DF，

∵，

∴，

∴，

∴AP＝2；

（3）解：由（2）知BD＝DF，

∵是等边三角形，PE⊥AB，

∴AE＝EF，

∴DE＝DF+EF

＝3，为定值，即DE的长不变．