题目内容
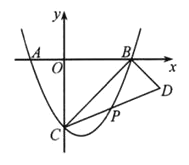
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
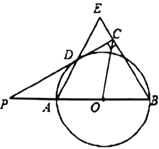
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)连接OD,由PD切 O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结论;(Ⅱ)由平行线的性质可得∠DOP=60°,利用三角函数可求出OD、OP、PC的长,即可得CD的长,利用勾股定理求出OC的长即可.
(Ⅰ)连接![]() ,
,
∵PD切![]() 于点
于点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅱ)∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴OD=2,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴DC=PC-PD=![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】学校组织甲、乙两组同学参加国学经典知识对抗赛,每组有![]() 位选手,每场比赛两组各派
位选手,每场比赛两组各派![]() 人进行现场对抗比赛,满分为
人进行现场对抗比赛,满分为![]() 分,共进行了
分,共进行了![]() 场比赛.学校整理和汇总了这
场比赛.学校整理和汇总了这![]() 场比赛的成绩,并制成如下所示的尚不完整的统计表和图所示的折线统计图.
场比赛的成绩,并制成如下所示的尚不完整的统计表和图所示的折线统计图.
场次 | 一 | 二 | 三 | 四 | 五 | 六 |
甲组成绩 (单位:分) |
|
|
|
|
|
|
乙组成绩 (单位:分) |
|
|
|
|
|
|
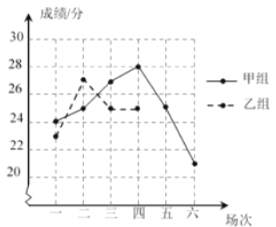
根据以上信息回答下面的问题:
(1)若甲、乙两组成绩的平均数相同,
①求![]() 的值;
的值;
②将折线统计图补充完整,并根据折线统计图判断哪组成绩比较稳定.
(2)若甲、乙两组成绩的中位数相等,直接写出![]() 的最小值.
的最小值.
(3)在(1)中的条件下,若从所有成绩为![]() 分的选手中随机抽取两人对其答题情况进行分析,请用列表法求抽到的两位选手均来自同一组的概率.
分的选手中随机抽取两人对其答题情况进行分析,请用列表法求抽到的两位选手均来自同一组的概率.
【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/千米 | 0.3元/分 | 0.8元/千米 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出部分每千米收0.8元. | |||
(1)小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点,他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.