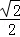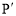Question

如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF＝∠ABC．

（1）求证：AB＝AC；

（2）若AD＝4，cos∠ABF＝，求DE的长．

 

 

Answer 1

（1）证明见解析；（2）.

【解析】

试题分析：（1）由BF是⊙O的切线，利用弦切角定理，可得∠ABF=∠C，又由∠ABF=∠ABC，可证得∠ABC=∠C.，即可得AB=AC.

（2）连接BD，在Rt△ADB中，解直角三角形求出AB的长度；然后在Rt△ABE中，解直角三角形求出AE的长度；最后利用求得结果.

（1）∵BF是⊙O的切线，∴∠ABF=∠C.

∵∠ABF=∠ABC，∴∠ABC=∠C.

∴AB=AC.

（2）如图，连接BD，在Rt△ADB中，∠BAD=90°，

∵，∴.

∴AB=3.

在Rt△ABE中，∠BAE=90°，

∵，∴.

∴.

∴.

考点：1.切线的性质；2.等腰三角形的判定；3.圆周角定理；4.锐角三角函数定义；5.勾股定理.