题目内容
1.选用适当方法解一元二次方程(1)(x-2)2=(2x+5)2
(2)(x2+3x)2-2(x2+3x)-8=0
(3)x2-2mx+m2-n2=0
(4)(m-1)x2+(m-2)x-1=0.
分析 (1)应用直接开平方法
(2)应用换元法
(3)将原方程变形:x2-2mx+m2=n2程后再用直接开平方法
(4)应用公式法
解答 (1)(x-2)2=(2x+5)2
解:两边同时开平方得:x-2=±(2x+5),即:
x-2=2x+5或x-2=-(2x+5)
解得:x1=-7,x2=-1
(2)(x2+3x)2-2(x2+3x)-8=0
解:令x2+3x=y,则原方程变为:y2-2y-8=0
解这个关于y一元二次方程得:y1=4,y2=-2
则:x2+3x=4或x2+3x=-2
解x2+3x=4得:x1=-4,x2=1,
解x2+3x=-2得:x3=-2,x4=-1
所以,原方程的解为:x1=-4,x2=1,x3=-2,x4=-1
(3)x2-2mx+m2-n2=0
解:将原方程变形:x2-2mx+m2=n2
则:(x-m)2=n2
所以:x-m=±n
故原方程的解为:x1=m+n,x2=m-n
(4)(m-1)x2+(m-2)x-1=0.
解:该方程为一元二次方程,故m-1≠0,
则△=(m-2)2+4(m-1)=m2
由求根公式x1,2=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$得:x2=$\frac{1}{m-1}$,x3=-1
故原方程的解为:x1=$\frac{1}{m-1}$,x2=-1
点评 本题考查了一元二次方程的解法,解题的关键是能够根据方程的结构特征选择适当的解法.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
6.如图,矩形ABCD中,AB=5,AD=4,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM,射线BN交线段CD于点F,则DF的最大值为( )
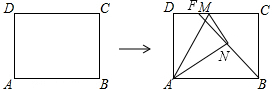

| A. | $\frac{5}{2}$ | B. | $\frac{24}{5}$ | C. | $\frac{12}{5}$ | D. | 2 |
 写出图中梯形ABCD各顶点的坐标.
写出图中梯形ABCD各顶点的坐标. 如图,AD为⊙O的直径,CD为弦,$\widehat{AB}$=$\widehat{BC}$,连接OB.
如图,AD为⊙O的直径,CD为弦,$\widehat{AB}$=$\widehat{BC}$,连接OB.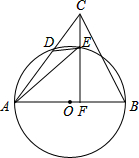 如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在$\widehat{BD}$上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在$\widehat{BD}$上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.