题目内容
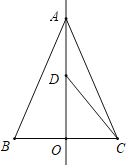
【题目】如图，等腰△ABC中，AB＝AC＝3，BC＝2，BC边上的高AO，点D为射线AO上一点，一动点P从点A出发，沿AD﹣DC运动，到达点C停止，动点P在AD上运动速度为3个单位每秒，动点P在CD上运动速度为1个单位每秒，则当AD＝____时，运动时间最短．
【答案】
【解析】
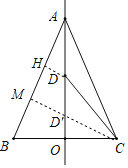
如图，作DH⊥AB于H，CM⊥AB于M，交AO于D′．运动时间t＝
+
＝+CD，由AHD∽△AOB，推出DH＝
AD，可得AD+CD＝CD+DH，推出当C，D，H共线且和CM重合时，运动时间最短．
解：如图，作DH⊥AB于H，CM⊥AB于M，交AO于D′．
∵运动时间t＝+＝+CD，
∵AB＝AC，AO⊥BC，
∴BO＝OC＝1，
∵∠DAH＝∠BAO，∠DHA＝∠AOB＝90°，
∴△AHD∽△AOB，
∴DH＝AD，
∴AD+CD＝CD+DH，
∴当C，D，H共线且和CM重合时，运动时间最短，
∵
，
BCAO＝ABCM，
∴CM＝
，
∴
，
∵AD′＝3MD′，设MD′＝m，则AD′＝3m，
则有：9m2﹣m2＝
，
∴m＝
或﹣(舍弃)，
∴AD′＝，
故答案为．
练习册系列答案
名校课堂系列答案
相关题目
