Question

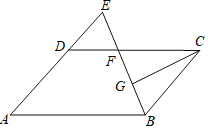
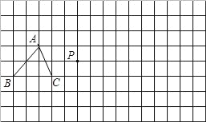
【题目】如图，已知△ABC中，∠BAC＝90°，AB＝AC＝6．D为BC边一点，且BD∶DC＝1∶2，以D为一个顶点作正方形DEFG，且DE＝BC，连接AE，将正方形DEFG绕点D旋转一周，在整个旋转过程中，当AE取得最大值时AG的长为______．

Answer 1

【答案】2

【解析】

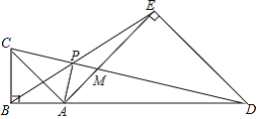
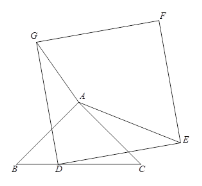
当点A、D、E在同一条直线上时，AE取得最大值，画出图形，过点A作AM⊥BC于点M，求出BC的长度，利用等腰直角三角形的性质和勾股定理，求出AD的长，进而可得AG的长．

解：当点A、D、E在同一条直线上时，AE取得最大值．
过点A作AM⊥BC于点M，

∵∠BAC=90°，AB=AC=6，
∴BC==6，
∴BM=CM=3，
∵BD：DC=1：2，DE=BC，
∴BD=2，DE=EF=DG=FG=6，
∴DM=32＝，
在Rt△ADM中，AD=，
在Rt△ADG中，AG=．
故答案为：2．