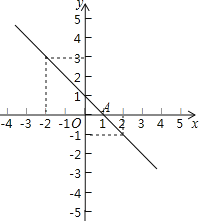题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,等腰直角三角形OAB的斜边AO在x轴上![]() ,
,![]() ,点B的坐标为
,点B的坐标为![]() .
.

(1)求A点坐标;
(2)过B作![]() 轴于C,点D从B出发沿射线BC以每秒2个单位的速度运动,连接AD、OD,动点D的运动时间为t,
轴于C,点D从B出发沿射线BC以每秒2个单位的速度运动,连接AD、OD,动点D的运动时间为t,![]() 的面积为S,求S与t的数量关系,并直接写出t的取值范围;
的面积为S,求S与t的数量关系,并直接写出t的取值范围;
(3)在(2)的条件下,当点D运动到x轴下方时,延长AB交y轴于E,过E作![]() 于H,在x轴正半轴上取点F,连接BF交EH于G,
于H,在x轴正半轴上取点F,连接BF交EH于G,![]() ,当
,当![]() 时,求点D的坐标.
时,求点D的坐标.
【答案】(1)A(﹣14,0);(2)S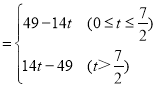 ;(3)D(﹣7,
;(3)D(﹣7,![]() )或(﹣7,﹣21).
)或(﹣7,﹣21).
【解析】
(1)作BH⊥OA于H.理由等腰直角三角形的性质求出OA即可解决问题;
(2)如图2中,分两种情形当0≤t![]() 时,当t
时,当t![]() 时,分别求解即可解决问题;
时,分别求解即可解决问题;
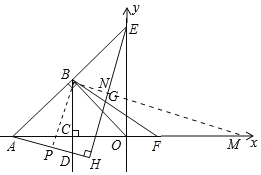
(3)如图3中,作BM∥AH交EH于N,BP⊥AD于P.理由相似三角形的性质证明EH=2AH,解直角三角形求出EH,AH,设H(m,n),构建方程组求出m,n,求出直线AH的解析式即可解决问题.
(1)作BH⊥OA于H.
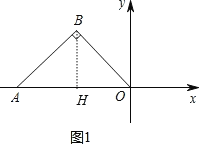
∵BA=BO,∠ABO=90°,∴BH=AH=OH.
∵B(﹣7,7),∴AH=BH=OH=7,∴OA=14,∴A(﹣14,0).
(2)如图2中,当0≤t![]() 时,S
时,S![]() 14×(7﹣2t)=49﹣14t
14×(7﹣2t)=49﹣14t
当t![]() 时,S
时,S![]() 14×(2t﹣7)=14t﹣49.
14×(2t﹣7)=14t﹣49.
综上所述:S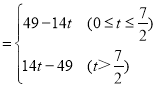 .
.
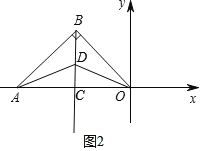
(3)如图3中,作BM∥AH交EH于N,BP⊥AD于P.
∵BP⊥AH,EH⊥AH,∴BP∥EH.
∵AB=BE,∴AP=PH,∴PB![]() EH.
EH.
∵BN∥AH,∴EN=NH,
∴BN![]() AH,∠BNG=∠BPD=90°.
AH,∠BNG=∠BPD=90°.
∵BM∥AH,∴∠BMF=∠MAH.
∵∠AFB=2∠OAD=∠FMB+∠FBM,
∴∠FBM=∠FMB=∠OAD.
∵∠OAD+∠ADC=90°,∠PBD+∠ADC=90°,
∴∠OAD=∠PBD,∴∠PBD=∠NBG.
∵∠BPD=∠BNG=90°,∴△BPD∽△BNG,
∴![]() 2,∴BP=2BN,∴EH=2AH.
2,∴BP=2BN,∴EH=2AH.
在Rt△AEH中,∵AE=14![]() ,EH=2AH,
,EH=2AH,
∴EH![]() ,AH
,AH![]() ,
,
设H(m,n),则有: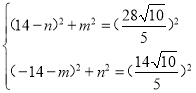 ,
,
解得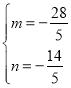 或
或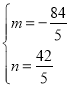 ,
,
∴H(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
易求直线AH的解析式为y![]() x
x![]() 或y=﹣3x﹣42,令x=-7,得:y=
或y=﹣3x﹣42,令x=-7,得:y=![]() 或﹣21,
或﹣21,
∴D(﹣7,![]() )或(﹣7,﹣21).
)或(﹣7,﹣21).