Question

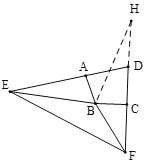
【题目】已知在四边形中，，，点，分别在射线，上，满足.

（1）如图1，若点，分别在线段，上，求证：；

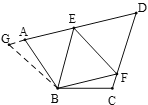
（2）如图2，若点，分别在线段延长线与延长线上，请直接写出与的数量关系.

Answer 1

【答案】（1）证明见解析；（2）∠EBF=90°+∠ADC.

【解析】

（1）如图，延长DA到G，使AG=CF，连接BG，根据及四边形内角和可得∠C+∠DAB=180°，可知∠C=∠GAB，利用SAS可证明△GAB≌△FCB，可得BG=BF，∠ABG=∠CBF，根据角的和差关系可得∠GBF=∠ABC，利用SSS可证明△GBE≌△FBE，可得∠GBE=∠EBF=∠ABC，根据即可得结论；（2）延长CD到H，使CH=AE，根据四边形内角和可得∠BCH=∠BAE，利用SAS可证明△BCH≌△BAE，可得BE=BH，∠ABE=∠HBC，根据角的和差关系可得∠EBH=∠ABC，根据EF=AE+CF可得EF=FH，利用SSS可证明△EBF≌△HBF，可得∠EBF=∠HBF，根据周角的定义即可得答案.

（1）如图，延长DA到G，使AG=CF，连接BG，

∵∠ABC+∠ADC=180°，

∴∠C+∠DAB=180°，

∵∠GAB+∠DAB=180°，

∴∠C=∠GAB，

在△GAB和△FCB中，，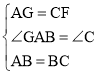

∴△GAB≌△FCB，

∴BG=BF，∠ABG=∠CBF，

∴∠ABF+∠ABG=∠ABF+∠CBF，即∠GBF=∠ABC，

∵EF=AE+CF，AG=CF，

∴EF=AE+AG=GE，

在△GBE和△FBE中，，

△GBE≌△FBE，

∴∠GBE=∠EBF，

∴∠EBF=∠GBF=∠ABC=(180°-∠ADC)=90°-∠ADC.

（2）延长CD到H，使CH=AE，

∵∠ABC+∠ADC=180°，

∴∠BCD+∠DAB=180°，

∵∠EAB+∠DAB=180°，

∴∠BCD=∠EAB，

在△BAE和△BCH中，，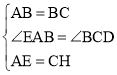

∴△BAE≌△BCH，

∴BE=BH，∠ABE=∠HBC，

∴∠ABE+∠ABH=∠HBC+∠ABH，即∠EBH=∠ABC，

∵EF=AE+CF，CH=AE，

∴EF=CH+CF=FH，

在△EBF和△HBF中，，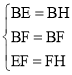

∴△EBF≌△HBF，

∴∠EBF=∠HBF，

∴∠EBF+∠FBH+∠EBH=2∠EBF+∠ABC=2∠EBF+(180°-∠ADC)=360°，

∴∠EBF=90°+∠ADC.