题目内容
菱形ABCD边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为( )
A.

B.

C.

D.

【答案】分析:根据菱形ABCD边长为4,∠BAD=60°求出菱形两条对角线的长度及ABE的边CF上的高、△BCF的边AE上的高,△DEF,进而求出菱形的面积及△ABE、△BCF的面积,然后根据AE+CF=4和∠ADC=120°,求出△CFD的面积;由图示可知:S△BEF=S菱形ABCD-S△ABE--S△BCF-S△DEF,代入数值根据二次函数的性质求出最值.
解答:解:∵菱形ABCD边长为4,∠BAD=60°;
∴△ABD与△BCD为正三角形;
∴BD=4,AC=4 ,△ABE的边AE上的高与△BCF的边CF上的高都为2
,△ABE的边AE上的高与△BCF的边CF上的高都为2 ,∠ADC=120;
,∠ADC=120;
设AE为x,则CF为4-x;
∴S△DEF= ED•DFsin120°=
ED•DFsin120°= (4-x)[4-(4-x)]
(4-x)[4-(4-x)] =-
=- x2+
x2+ x;
x;
由图示可知:S△BEF=S菱形ABCD-S△ABE--S△BCF-S△DEF
= ×4×4
×4×4 -
- CF-
CF- AE-S△DEF
AE-S△DEF
=8 -
- (CF+AE)-S△DEF
(CF+AE)-S△DEF
=8 -4
-4 S△DEF
S△DEF
= x2-
x2- x+4
x+4 ;
;
根据二次函数的性质,△BEF面积的最小值= =
= =
= =3
=3 .
.
故选B.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.此题结合面积和锐角三角函数知识解答,是一道好的综合题.
解答:解:∵菱形ABCD边长为4,∠BAD=60°;
∴△ABD与△BCD为正三角形;
∴BD=4,AC=4
 ,△ABE的边AE上的高与△BCF的边CF上的高都为2
,△ABE的边AE上的高与△BCF的边CF上的高都为2 ,∠ADC=120;
,∠ADC=120;设AE为x,则CF为4-x;
∴S△DEF=
 ED•DFsin120°=
ED•DFsin120°= (4-x)[4-(4-x)]
(4-x)[4-(4-x)] =-
=- x2+
x2+ x;
x;由图示可知:S△BEF=S菱形ABCD-S△ABE--S△BCF-S△DEF
=
 ×4×4
×4×4 -
- CF-
CF- AE-S△DEF
AE-S△DEF=8
 -
- (CF+AE)-S△DEF
(CF+AE)-S△DEF=8
 -4
-4 S△DEF
S△DEF=
 x2-
x2- x+4
x+4 ;
;根据二次函数的性质,△BEF面积的最小值=
 =
= =
= =3
=3 .
.故选B.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.此题结合面积和锐角三角函数知识解答,是一道好的综合题.

练习册系列答案
相关题目
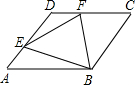 菱形ABCD边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为( )
菱形ABCD边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为( )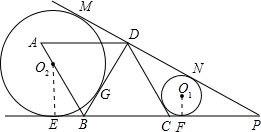 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G. 的值是
▲ .
的值是
▲ .