题目内容
菱形ABCD边长为4，点E在直线AD上，DE=3，连接BE与对角线AC交点M，那么| AM | MC |
分析：根据菱形的性质，可得对边平行，即可得到△AME∽△CMB，注意作图时需要分析点E在线段AD上还是在线段AD的延长线上．
解答：解：①如图：
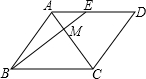
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AME∽△CMB，
∴
=
，
∵DE=3，
∴AE=AD-DE=1，
∴
=
，
②如图：
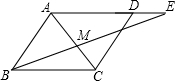
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AME∽△CMB，
∴
=
，
∵DE=3，
∴AE=AD+DE=7，
∴
=
，
故答案为：
或
．
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AME∽△CMB，
∴
| AE |
| BC |
| AM |
| MC |
∵DE=3，
∴AE=AD-DE=1，
∴
| AM |
| MC |
| 1 |
| 4 |
②如图：
∵四边形ABCD是菱形，
∴AD=BC=4，AD∥BC，
∴△AME∽△CMB，
∴
| AE |
| BC |
| AM |
| MC |
∵DE=3，
∴AE=AD+DE=7，
∴
| AM |
| MC |
| 7 |
| 4 |
故答案为：
| 1 |
| 4 |
| 7 |
| 4 |
点评：此题考查了相似三角形的判定与性质，以及菱形的性质．解此题的关键是注意分类讨论思想与数形结合思想的应用．
练习册系列答案
相关题目
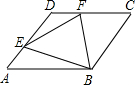菱形ABCD边长为4，∠BAD=60°，点E是AD上一动点（不与A、D重合），点F是CD上一动点，AE+CF=4，则△BEF面积的最小值为（ ）
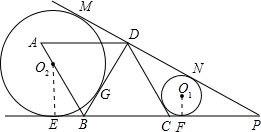上，半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N，半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G．
的值是
▲ .