题目内容
如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D:(1)求证:DA=DC;
(2)当DF:EF=1:8,DF=
 时,求AB•AC的值.
时,求AB•AC的值.
【答案】分析:(1)连接OC,构建等腰三角形OBC,由等腰三角形的性质知∠1=∠2;然后由切线的性质及直角三角形的两个锐角互余的性质求得∠3=∠4,因为等角对等边,所以DA=DC;
(2)由切割线定理知CD2=DF•DE,所以CD=AD=3 ;从而求得AF=3
;从而求得AF=3 -
- =2
=2 ,AE=6
,AE=6 ;最后根据相交弦定理求得AB•AC=AE•AF=24.
;最后根据相交弦定理求得AB•AC=AE•AF=24.
解答: 解:(1)连接OC,则有∠1=∠2(1分),
解:(1)连接OC,则有∠1=∠2(1分),
又CD是切线,∴OC⊥CD,(1分)
而∠4与∠1互余,∠3与∠2互余,
∴∠3=∠4,
∴DA=DC(2分)
(2)∵DF= ,
,
∴EF=8 (1分),
(1分),
又∵CD2=DF•DE= =18,
=18,
∴CD=3 =AD(1分)
=AD(1分)
∴AF=3 -
- =2
=2 ,AE=6
,AE=6 (1分)
(1分)
∴AB•AC=AE•AF=24.(1分)
点评:本题综合考查了切线的性质、垂径定理、相交弦定理、切割线定理.解答该题的关键是通过作辅助线OC,利用圆的性质构造等腰三角形.
(2)由切割线定理知CD2=DF•DE,所以CD=AD=3
 ;从而求得AF=3
;从而求得AF=3 -
- =2
=2 ,AE=6
,AE=6 ;最后根据相交弦定理求得AB•AC=AE•AF=24.
;最后根据相交弦定理求得AB•AC=AE•AF=24.解答:
 解:(1)连接OC,则有∠1=∠2(1分),
解:(1)连接OC,则有∠1=∠2(1分),又CD是切线,∴OC⊥CD,(1分)
而∠4与∠1互余,∠3与∠2互余,
∴∠3=∠4,
∴DA=DC(2分)
(2)∵DF=
 ,
,∴EF=8
 (1分),
(1分),又∵CD2=DF•DE=
 =18,
=18,∴CD=3
 =AD(1分)
=AD(1分)∴AF=3
 -
- =2
=2 ,AE=6
,AE=6 (1分)
(1分)∴AB•AC=AE•AF=24.(1分)
点评:本题综合考查了切线的性质、垂径定理、相交弦定理、切割线定理.解答该题的关键是通过作辅助线OC,利用圆的性质构造等腰三角形.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
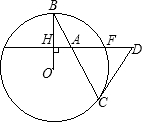 如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D:
如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D: 12、如图,已知OB是⊙O的半径,点C、D在⊙O上,∠DCB=40°,则∠OBD=
12、如图,已知OB是⊙O的半径,点C、D在⊙O上,∠DCB=40°,则∠OBD= 如图,已知OB是⊙O的半径,点C、D在⊙O上,∠DCB=40°,则∠OBD=( )
如图,已知OB是⊙O的半径,点C、D在⊙O上,∠DCB=40°,则∠OBD=( ) 如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D:
如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D: 时,求AB•AC的值.
时,求AB•AC的值.