题目内容
16.化简:$\frac{2}{m+1}$-$\frac{m-2}{{m}^{2}-1}$÷(1-$\frac{1}{{m}^{2}-2m+1}$)分析 原式第二项括号中通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{2}{m+1}$-$\frac{m-2}{(m+1)(m-1)}$÷$\frac{{m}^{2}-2m+1-1}{{m}^{2}-2m+1}$
=$\frac{2}{m+1}$-$\frac{m-2}{(m+1)(m-1)}$•$\frac{(m-1)^{2}}{m(m-2)}$
=$\frac{2}{m+1}$-$\frac{m-1}{m(m+1)}$
=$\frac{2m-m+1}{m(m+1)}$
=$\frac{m+1}{m(m+1)}$
=$\frac{1}{m}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.十边形的内角和为( )
| A. | 360° | B. | 1440° | C. | 1800° | D. | 2160° |
11.若一个三角形的三条边长分别为3,2a-1,6,则整数a的值可能是( )
| A. | 2,3 | B. | 3,4 | C. | 2,3,4 | D. | 3,4,5 |
1.下列调查中,最合适采用抽样调查的是( )
| A. | 乘坐高铁对旅客的行李的检查 | |
| B. | 了解抚顺市民对春节晚会节目的满意程度 | |
| C. | 调查九年一班全体同学的身高情况 | |
| D. | 对新研发的新型战斗机的零部件进行检查 |
 如图,△ABC的三个顶点都在⊙O上,AD是直径,且∠CAD=56°,则∠B的度数为34°.
如图,△ABC的三个顶点都在⊙O上,AD是直径,且∠CAD=56°,则∠B的度数为34°.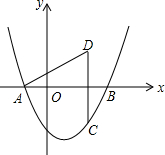 如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),
如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧), 如图,半径为1的⊙P在射线AB上运动,且A(-3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是(-2,1)或(-1,2)或(1,4).
如图,半径为1的⊙P在射线AB上运动,且A(-3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是(-2,1)或(-1,2)或(1,4).