题目内容
如图,抛物线y=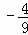 x2通过平移得到抛物线m,抛物线m经过点B(6,0)和O(0,0),它的顶点为A
x2通过平移得到抛物线m,抛物线m经过点B(6,0)和O(0,0),它的顶点为A ,以O为圆心,OA为半径作圆,在第四象限内与抛物线y=
,以O为圆心,OA为半径作圆,在第四象限内与抛物线y=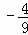 x2交于点C,连接AC,则图中阴影部分的面积为
x2交于点C,连接AC,则图中阴影部分的面积为

 ﹣12.
﹣12.
【解析】∵抛物线m经过点B(6,0)和O(0,0),∴抛物线m的对称轴为直线x=3,
∵抛物线y= x2通过平移得到抛物线m,∴设抛物线m的解析式为y=
x2通过平移得到抛物线m,∴设抛物线m的解析式为y= (x﹣3)2+k,
(x﹣3)2+k,
将O(0,0)代入,得 (0﹣3)2+k=0,解得k=4,
(0﹣3)2+k=0,解得k=4,
∴抛物线m的解析式为y= (x﹣3)2+4,顶点A的坐标为(3,4),
(x﹣3)2+4,顶点A的坐标为(3,4),
由勾股定理,得OA=5.
连接OA、OC,由圆的对称性或垂径定理,可知C的坐标为(3,﹣4),
阴影部分的面积=半圆的面积﹣△AOC的面积= •π•52﹣
•π•52﹣ ×8×3=
×8×3= ﹣12.
﹣12.

练习册系列答案
相关题目
 的图象位于第一、第三象限,则k的取值范围是
的图象位于第一、第三象限,则k的取值范围是 ,且使关于x的不等式组
,且使关于x的不等式组 有解的概率为 .
有解的概率为 . 的值为( )
的值为( )
 B.3 C.
B.3 C.
 ,当点
,当点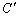 落在BC的延长线上时,线段
落在BC的延长线上时,线段 交BC于点E,则线段
交BC于点E,则线段 的长度为 .
的长度为 .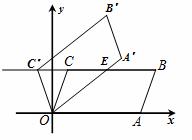
 进一批价格分别为80元、60元的篮球和足球。该校打算用1000元购买篮球和足球
进一批价格分别为80元、60元的篮球和足球。该校打算用1000元购买篮球和足球 ,问恰好用完1000元
,问恰好用完1000元 ,并且篮球、足球都买有的购买方案有哪几种?
,并且篮球、足球都买有的购买方案有哪几种? 当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需
当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需  秒.
秒.
