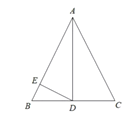
题目内容
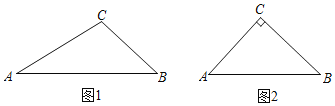
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,
边上的中线,![]() 于点
于点![]()
(1)求证:BD·AD=DE·AC.
(2)若AB=13,BC=10,求线段DE的长.
(3)在(2)的条件下,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先利用等腰三角形的性质证明∠B=∠C,AD⊥BC,然后再证明△BDE∽△CAD即可;
(2)利用勾股定理求出AD,再根据(1)的结论即可求出DE;
(3)在Rt△BDE中,利用锐角三角函数求解即可.
解:(1)证明:∵AB=AC, AD为BC边上的中线,
∴∠B=∠C,AD⊥BC,即∠ADC=90°,
又∵DE⊥AB于点E,即∠DEB=90°,
∴∠ADC=∠DEB,
∴△BDE∽△CAD,
∴![]() ,
,
∴BD·AD=DE·AC;
(2)∵AD为BC边上的中线,BC=10,
∴BD=CD=5,
在Rt△ABD中,AB=13,BD=5,
∴AD= ![]() ,
,
由(1)得BD·AD=DE·AC,
又∵AC=AB= 13,
∴5×12=13·DE,
∴DE=![]() ;
;
(3)由(2)知,DE=![]() ,BD=5,
,BD=5,
∴在Rt△BDE中,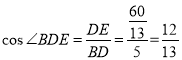 .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】为了解早高峰期间A,B两邻近地铁站乘客的乘车等待时间(指乘客从进站到乘上车的时间),某部门在同一上班高峰时段对A、B两地铁站各随机抽取了500名乘客,收集了其乘车等待时间(单位:分钟)的数据,统计如表:
等待时的频数间 乘车等待时间 地铁站 | 5≤t≤10 | 10<t≤15 | 15<t≤20 | 20<t≤25 | 25<t≤30 | 合计 |
A | 50 | 50 | 152 | 148 | 100 | 500 |
B | 45 | 215 | 167 | 43 | 30 | 500 |
据此估计,早高峰期间,在A地铁站“乘车等待时间不超过15分钟”的概率为_____;夏老师家正好位于A,B两地铁站之间,她希望每天上班的乘车等待时间不超过20分钟,则她应尽量选择从_____地铁站上车.(填“A”或“B”)