题目内容
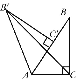
【题目】如图1，在
和
中，顶点
是它们的公共顶点，
，
．
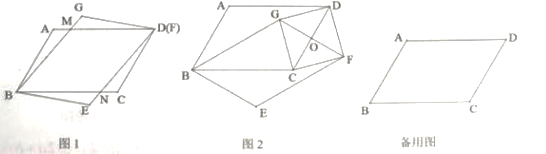
（特例感悟）（1）当顶点
与顶点
重合时（如图1），
与
相交于点
，
与
相交于点
，求证：四边形
是菱形；
（探索论证）（2）如图2，当
时，四边形
是什么特殊四边形？试证明你的结论；
（拓展应用）（3）试探究：当
等于多少度时，以点
为顶点的四边形是矩形？请给予证明．
【答案】(1)见解析； (2)当∠GBC=30°时，四边形GCFD是正方形．证明见解析；(3)当∠GBC=120°时，以点
，
，
，
为顶点的四边形CGFD是矩形. 证明见解析．
【解析】
（1）先证明四边形
是平行四边形，再通过证明
得出
，从而证明四边形是菱形；
（2）证法一：如图，连接
交
于
，在
上取一点
，使得
，通过证明
，
，
，从而证明当∠GBC=30°时，四边形GCFD是正方形；
证法二：如图，过点G作GH⊥BC于H，通过证明OD=OC=OG=OF，GF=CD，从而证明当∠GBC=30°时，四边形GCFD是正方形；
（3）当∠GBC=120°时，点E与点A重合，通过证明
，CD=GF，
，从而证明四边形
是矩形．
(1) 
，
，
四边形是平行四边形，
在
和
中，
，
，
四边形是菱形．
(2)当∠GBC=30°时，四边形GCFD是正方形．
证法一：如图，连接交于，在上取一点，使得，
，
，
，
，
，
，
.
，
，
，
，
，
，
，
，
设
，则
，
，
在Rt△BGK中，
，解得
，
，
，
，
，
，
，，
四边形
是平行四边形，
，
四边形是矩形，
，
四边形是正方形．
证法二：如图
∵，
.
又，
，
，
.
过点G作GH⊥BC于H，
在Rt△BHG中，
∵，
∴GH=
BG＝
＋１，BH＝GH＝3＋，
∴HC=BC﹣BH=2+2-（3＋）=-1，
∴GC=
，
∴OG=OC=
=
=2，
∴OD=OF=4-2=2，
∴OD=OC=OG=OF，
四边形是矩形，
∵GF=CD，
四边形是正方形．
(3) 当∠GBC=120°时，以点，，，为顶点的四边形CGFD是矩形.
当∠GBC=120°时，点E与点A重合.
，
∴
，
.
∵四边形ABCD和四边形GBEF是平行四边形，
∴
，
，AB=CD，AB=GF，
∴，CD=GF，
四边形是平行四边形.
∵，
四边形是矩形．
