题目内容
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
A. 2 B. 4 C. 2 D. 4
D. 4

C
解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2 ,即DQ+PQ的最小值为2
,即DQ+PQ的最小值为2 .
.


练习册系列答案
相关题目
 的解都不大于1.
的解都不大于1. .
. ﹣2,则x6+3x5+11x3+2x+1=
﹣2,则x6+3x5+11x3+2x+1= 
 ,PE⊥PB交CD于点E,则PE= .
,PE⊥PB交CD于点E,则PE= .
 .
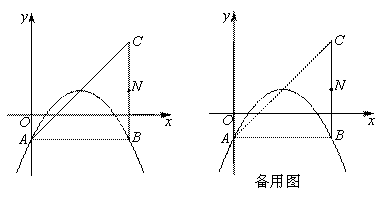
.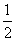 x2+bx+c (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.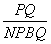 取最大值时,点Q的坐标为________.
取最大值时,点Q的坐标为________.