题目内容
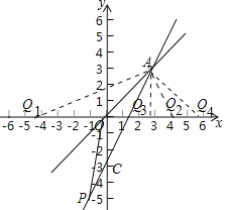
【题目】在平面直角坐标系中,直线l1的函数关系式为y=2x+b,直线l2过原点且与直线l1交于点P(-1,-5).
(1)试问(-1,-5)可以看作是怎样的二元一次方程组的解?
(2)设直线l1与直线y=x交于点A,求△APO的面积;
(3)在x轴上是否存在点Q,使得△AOQ是等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)(-1,-5)可以看成二元一次方程组![]() 的解;(2)S△AOP=6;(3)存在,点Q坐标为(-3
的解;(2)S△AOP=6;(3)存在,点Q坐标为(-3![]() ,0)或(3,0)或(3
,0)或(3,0)或(3![]() ,0)或(6,0).
,0)或(6,0).
【解析】
(1)求出直线![]() 与直线
与直线![]() 的解析式即可解决问题;
的解析式即可解决问题;
(2)利用方程组求出点A坐标,再求出直线![]() 与y轴的交点C的坐标,然后根据
与y轴的交点C的坐标,然后根据![]() 计算即可;
计算即可;
(3)根据等腰三角形的定义,分![]() 三种情形,然后利用两点之间的距离公式分别求解即可.
三种情形,然后利用两点之间的距离公式分别求解即可.
(1)∵点![]() 在直线
在直线![]() 上
上
![]() ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
设直线![]() 的解析式为
的解析式为![]()
则有![]() ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
故![]() 可以看成二元一次方程组
可以看成二元一次方程组![]() 的解;
的解;
(2)由![]() ,解得
,解得![]()
![]()
∵点![]() 在直线
在直线![]() 上,直线
上,直线![]() 交y轴于
交y轴于![]()
![]()
故![]() 的面积为6;
的面积为6;
(3)![]()
![]()
设点Q坐标为![]()
由等腰三角形的定义,分以下三种情况:
①当![]() 时,则
时,则![]() ,即
,即![]()
②当![]() 时,则
时,则![]()
解得![]() ,即
,即![]()
③当![]() 时,则
时,则![]()
解得![]() 或
或![]() (与点O重合,舍去),即
(与点O重合,舍去),即![]()
综上,满足条件的点Q坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目