题目内容
14.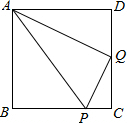 已知:如图,在正方形ABCD中,BP=3PC,Q是CD的中点.求证:△PQC∽△QAD∽△PAQ.
已知:如图,在正方形ABCD中,BP=3PC,Q是CD的中点.求证:△PQC∽△QAD∽△PAQ.
分析 先根据四边形ABCD是正方形,BP=3PC,Q是CD的中点得出QC=QD=$\frac{1}{2}$AD,CP=$\frac{1}{4}$AD,再由相似三角形的判定定理即可得出结论.
解答 证明:∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴QC=QD=$\frac{1}{2}$AD,CP=$\frac{1}{4}$AD,
∴$\frac{AD}{QC}$=$\frac{DQ}{CP}$=2,
又∵∠ADQ=∠QCP,
∴△PQC∽△QAD.
∴$\frac{AQ}{PQ}$=$\frac{CQ}{PC}$=2,∠DAQ=∠CQP.
∵∠DAQ+∠AQD=90°,
∴∠AQD+∠PQC=90°,
∴∠AQP=∠C=90°,
∴△PAQ∽△PQC,
∴△PQC∽△QAD∽△PAQ.
点评 本题考查的是相似三角形的判定与性质,熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目




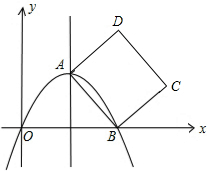 如图,已知正方形ABCD的顶点C,D的坐标分别是(8,2),(6,6),点B落在x轴上,若抛物线y=-2x2+bx+c经过点A和点B,则b的值为( )
如图,已知正方形ABCD的顶点C,D的坐标分别是(8,2),(6,6),点B落在x轴上,若抛物线y=-2x2+bx+c经过点A和点B,则b的值为( )
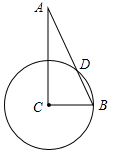 如图,在Rt△ABC中,∠ACB=90°,AB=2BC,以C为圆心,以CB为半径的圆交AB于点D,求$\widehat{BD}$的度数.
如图,在Rt△ABC中,∠ACB=90°,AB=2BC,以C为圆心,以CB为半径的圆交AB于点D,求$\widehat{BD}$的度数.