Question

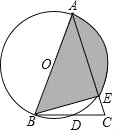
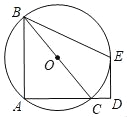
【题目】如图，已知△ABC内接于⊙O，BC为⊙O直径，延长AC至D，过D作⊙O切线，切点为E，且∠D＝90°，连接BE．DE＝12，

（1）若CD＝4，求⊙O的半径；

（2）若AD+CD＝30，求AC的长．

Answer 1

【答案】（1）20；（2）18.

【解析】

(1) （2） 连接OE，作OH⊥AD于H，利用切线性质和垂径定理、矩形的判定和性质、勾股定理即可解答；

（1）解：连接OE，作OH⊥AD于H，

∵DE是⊙O的切线，

∴OE⊥DE．

又∵∠D＝90°，

∴四边形OHDE是矩形，

设⊙O的半径为r，

在Rt△OCH中，

OC2＝CH2+OH2，

∴r2＝（r﹣4）2+144，

∴半径r＝20．

（2）解：∵OH⊥AD，

∴AH＝CH．

又∵AD+CD＝30，即：（AH+HD）+（HD﹣CH）＝30．

∴2HD＝30，HD＝15，即OE＝HD＝OC＝15，

∴在Rt△OCH中，CH＝ ＝＝9．

∴AC＝2CH＝18．