题目内容
19. 如图,已知AD∥EF∥BC,AE=4,EB=6,DF=3
如图,已知AD∥EF∥BC,AE=4,EB=6,DF=3(1)则$\frac{DF}{FC}$=$\frac{2}{3}$;
(2)求DC的长.
分析 (1)由AD∥EF∥BC,AE=4,EB=6,根据平行线分线段成比例定理,即可求得$\frac{DF}{FC}$=$\frac{2}{3}$;
(2)由AD∥EF∥BC,AE=4,EB=6,DF=3,根据平行线分线段成比例定理,即可求得DF的长,则$DC=DF+FC=3+\frac{9}{2}=\frac{15}{2}$.
解答  解:(1)∵AD∥EF∥BC,
解:(1)∵AD∥EF∥BC,
∴$\frac{AE}{BE}$=$\frac{DF}{FC}$,
∵AE=4,EB=6,
∴$\frac{DF}{FC}$=$\frac{2}{3}$,
故答案是:$\frac{2}{3}$;
(2)∵AD∥EF∥BC,
∴$\frac{AE}{EB}=\frac{DF}{FC}$,
∵AE=4,EB=6,DF=3,
∴$\frac{4}{6}=\frac{3}{FC}$.
∴$FC=\frac{9}{2}$.
∴$DC=DF+FC=3+\frac{9}{2}=\frac{15}{2}$,
∴DC的长是$\frac{15}{2}$.
点评 此题考查了平行线分线段成比例定理.此题难度适中,注意数形结合思想的应用.

练习册系列答案
相关题目
10.下列说法错误的是( )
| A. | 2x2-3xy-1是二次三项式 | B. | -x+1不是单项式 | ||
| C. | -$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$π | D. | -22xyb2的次数是6 |
11.从重庆北开往北京的特快车,途中要停靠四个站点,如果任意两个间的票价不同,那么不同票价有( )种.
| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
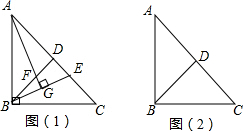 如图(1),已知等腰直角△ABC中,BD为斜边上的中线,E为DC上的一点,且AG⊥BE于G,AG交BD于F.
如图(1),已知等腰直角△ABC中,BD为斜边上的中线,E为DC上的一点,且AG⊥BE于G,AG交BD于F.