题目内容
11.先化简,再求值:$\frac{{a}^{2}-2ab}{a-b}$-$\frac{{b}^{2}}{b-a}$,其中a=1+$\sqrt{3}$,b=-1+$\sqrt{3}$.分析 原式变形后,利用同分母分式的加法法则计算,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-2ab+{b}^{2}}{a-b}$=$\frac{(a-b)^{2}}{a-b}$=a-b,
当a=1+$\sqrt{3}$,b=-1+$\sqrt{3}$时,原式=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列各组中,不是同类项的是( )
| A. | 52与25 | B. | -ab与ba | C. | 0.2a2b与-$\frac{1}{5}$a2b | D. | a2b3与-a3b2 |
20.正比例函数y=-2x的图象经过的点是( )
| A. | (1,2) | B. | (1,-2) | C. | (-2,1) | D. | (-2,-1) |
1.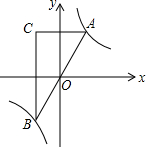 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )| A. | n=-2m | B. | n=-$\frac{2}{m}$ | C. | n=-4m | D. | n=-$\frac{4}{m}$ |
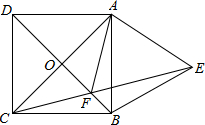 已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.
已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.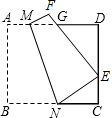 如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.
如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.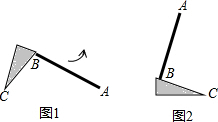 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.