��Ŀ����
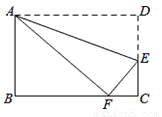
��ͼ���ھ���ABCD�У�AB=3��AD=5����E��DC�ϣ�������ABCD��AE�۵�����Dǡ������BC���ϵĵ�F������ôcos��EFC��ֵ�ǣ�������
A. 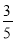 B.
B. 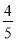 C.
C. 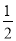 D.
D. 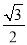
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
��Ŀ����
��ͼ���ھ���ABCD�У�AB=3��AD=5����E��DC�ϣ�������ABCD��AE�۵�����Dǡ������BC���ϵĵ�F������ôcos��EFC��ֵ�ǣ�������

A. 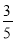 B.
B. 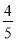 C.
C. 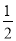 D.
D. 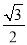
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�