题目内容
已知函数y=
+x,下列结论中正确的是( )
| 6-x |
A、有最大值
| ||
B、有最小值
| ||
C、有最大值
| ||
D、有最小值
|
考点:二次函数的最值
专题:计算题
分析:利用换元法,设
=t,则x=6-t2,所以y=t+6-t2,然后配方得到y=-(t-
)2+
,然后根据二次函数的最值问题求解.
| 6-x |
| 1 |
| 2 |
| 25 |
| 4 |
解答:解:设
=t,则6-x=t2,即x=6-t2,
y=t+6-t2
=-(t-
)2+
,
所以当t=
时,y有最大值
.
故选A.
| 6-x |
y=t+6-t2
=-(t-
| 1 |
| 2 |
| 25 |
| 4 |
所以当t=
| 1 |
| 2 |
| 25 |
| 4 |
故选A.
点评:本题考查了二次函数y=ax2+bx+c的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-
时,y=
.当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-
时,y=
.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
下列分式中不是最简分式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
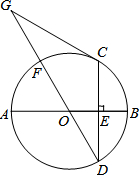 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30.
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30.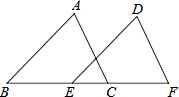 如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=70°,求∠ACB的度数.
如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=70°,求∠ACB的度数.