题目内容
18.在方程组$\left\{\begin{array}{l}{2x+y=1-m}\\{x+2y=2}\end{array}\right.$中,若未知数x、y满足x+y>0,则m的取值范围应为( )| A. | m<3 | B. | m>3 | C. | m<0 | D. | m>0 |
分析 将方程组中两方程相加,便可得到关于x+y的方程,再根据x+y>0,即可求出m的取值范围.
解答 解:$\left\{\begin{array}{l}{2x+y=1-m}\\{x+2y=2}\end{array}\right.$,
①+②得,(2x+y)+(x+2y)=(1-m)+2,
即3x+3y=3-m,
可得x+y=$\frac{3-m}{3}$,
∵x+y>0,
∴$\frac{3-m}{3}$>0,
解得m<3,
故选A.
点评 此题考查的是二元一次方程组和不等式的性质,要注意x+y>0,则解出x,y关于m的式子,最终求出m的取值范围.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
9.2014年春晚小品《扶不扶》一时成为大家讨论的热点,于是某校七(2)班共有50名同学对老人自己不慎摔倒扶不扶,提出了4种不同观点,经统计得出了如下统计表和统计图,请根据图表中提供的信息解答下列问题:

(1)填空:a=25,b=5,c=5;
(2)请分别补全两个统计图;
(3)在图2中,求代表B组“观点”的扇形圆心角度数.
| 组别 | 观点 | 频数(人数) |
| A | 应立即扶起,并送医院 | a |
| B | 应赶快离开,省得惹事 | 15 |
| C | 应只看热闹,不要行动 | b |
| D | 要老人走路小心,但不能扶 | c |

(1)填空:a=25,b=5,c=5;
(2)请分别补全两个统计图;
(3)在图2中,求代表B组“观点”的扇形圆心角度数.
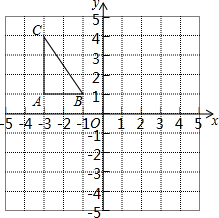 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.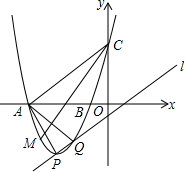 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1. 小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与他时间的变化情况,如图所示.
小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与他时间的变化情况,如图所示.