题目内容
4.己知一组数据为:3,4,4,6,8.计算这组数据的平均数和方差.分析 先把这组数据的5个数字加起来求和,再除以5即可求出这组数据的平均数,然后再根据方差公式s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]求解即可.
解答 解:(3+4+4+6+8)÷5=25÷5=5,
s2=$\frac{1}{5}$[(3-5)2+(4-5)2+(4-5)2+(6-5)2+(8-5)2]=$\frac{16}{5}$=3.2.
故这组数据的平均数为5,方差为3.2.
点评 本题考查了平均数和方差公式,解题时牢记公式是关键,此题比较简单,只要牢记公式即可正确求解.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
12.下列计算正确的是( )
| A. | a6÷a2=a3 | B. | (a2)3=a5 | C. | a0=0 | D. | a-3=$\frac{1}{{a}^{3}}$ |
19.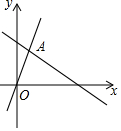 如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )| A. | $x<\frac{3}{2}$ | B. | $x>\frac{3}{2}$ | C. | x<3 | D. | x>3 |
16.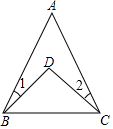 如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )
如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )
 如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )
如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )| A. | 75° | B. | 95° | C. | 105° | D. | 115° |
13.对整式3x2-12y2因式分解正确的是( )
| A. | 3(x2-4y2) | B. | 3(x+2y)(x-2y) | C. | 3(2x+y)(2x-y) | D. | 3(x-2y)2 |
 如图,某校要在长为32m,宽为20m的长方形操场上修筑宽度相同的道路(图中阴影部分),在余下的空白部分种上草坪,要使草坪的面积为540m2,求道路的宽.
如图,某校要在长为32m,宽为20m的长方形操场上修筑宽度相同的道路(图中阴影部分),在余下的空白部分种上草坪,要使草坪的面积为540m2,求道路的宽.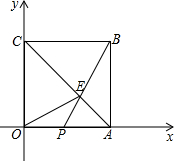 如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.
如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.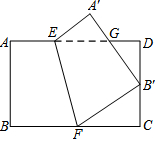 将矩形ABCD沿EF折叠,使点B与CD边中点B′重合,A′B′交AD于点G,若AE=1,AB=2,BC=3,下面有4个结论中,正确的个数是( )
将矩形ABCD沿EF折叠,使点B与CD边中点B′重合,A′B′交AD于点G,若AE=1,AB=2,BC=3,下面有4个结论中,正确的个数是( )