Question

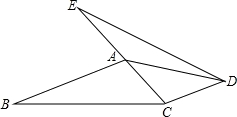
如图，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，AC=26，BD=24，则线段MN长为__________．

Answer 1

5【考点】直角三角形斜边上的中线；等腰三角形的判定与性质；勾股定理．

【分析】根据在直角三角形中，斜边上的中线等于斜边的一半得到BM=DM=5，根据等腰三角形的性质得到BN=4，根据勾股定理得到答案．

【解答】解：连接BM、DM，

∵∠ABC=∠ADC=90°，M是AC的中点，

∴BM=AC，DM=AC，

∴BM=DM=13，又N是BD的中点，

∴BN=DN=BD=12，

∴MN==5，

故答案为：5．

【点评】本题考查的是直角三角形的性质、等腰三角形的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．