��Ŀ����
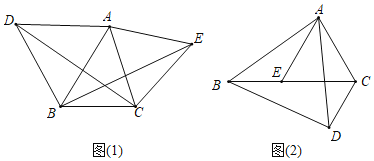
����Ŀ����1����֪����ͼ��1�����ڡ�ABC�У��ֱ���AB��ACΪ���ڡ�ABC�ⲿ���ȱ������Ρ�ABD����ACE������CD��BE����֤��BE��DC��
��2��Ӧ�ã���ͼ��2�����ڡ�ABC�У�AB��AC���ֱ���AB��ACΪ���ڡ�ABC�ڲ������������Ρ�ABD����ACE����Eǡ����BC���ϣ�ʹAB��AD��AC��AE���ҡ�BAD����CAE������CD��CE��3cm��CD��2cm����ABC�����Ϊ25cm2�����ABE�������
���𰸡���1��֤������������2����ABE�������10cm2��
��������
̽����֤����ADC�ա�ABE��SAS�����ɵ�BE��DC��
Ӧ�ã���A������ABC�ĸ��ߣ�����ΪF����֤����ADC�ա�ABE���ɵ�BE��DC��2������������AF��10�����ABE������������
��֪��֤�����ߡ�ABD�͡�ACEΪ�ȱ������Σ�
���EAC����DAB��60�㣬
���DAB+��BAC����EAC+��CAB��
���DAC����EAB��
��AD��AB��AC��AE��
���ADC�ա�ABE��SAS����
��BE��DC��
Ӧ�ã��⣺��A������ABC�ĸ��ߣ�����ΪF��

�ߡ�BAD����EAC��
���BAD����EAD����EAC����EAD��
���BAE����DAC��
��AB��AD��AE��AC
���ABE�ա�ADC��SAS����
��DC��BE��2��
��EC��3��
��BC��5��
�ߡ�ABC�������25cm2��
��![]() ��
��
��AF��10��
���ABE�������![]() ��10cm2
��10cm2
���ABE�������10cm2��





