Question

【题目】已知二次函数y = 2x2 -4x -6.

（1）用配方法将y = 2x2 -4x -6化成y = a (x - h) 2 + k的形式；并写出对称轴和 顶点坐标。

（2）在平面直角坐标系中，画出这个二次函数的图象；

（3）当时，求y的取值范围；

（4）求函数图像与两坐标轴交点所围成的三角形的面积。

Answer 1

【答案】（1） 对称轴是直线x=1， 顶点坐标是（1，-8）；（2）图象见解析；（3）；（4）12.

【解析】

（1）先提取公因式2，然后再利用配方法将原式变形为y=2（x-1）2-8，最后再求得抛物线的对称和顶点坐标即可；

（2）根据二次函数画图即可；
（3）当x=1时，y有最小值，当x=4时，y有最大值，从而可求得y的范围；
（4）先求得抛物线与x轴、y轴的交点坐标，最后依据三角形的面积公式求解即可．

（1）y=2x2-4x-6
=2（x2-2x+1）-2-6
=2（x-1）2-8；

对称轴是直线x=1， 顶点坐标是（1，-8）；
（2）令x=0，得y=-6，
令y=0，得2x2-4x-6=0，解得x=-1或x=3，
则抛物线与x轴的交点为：（-1，0），（3，0）；与y轴的交点为：（0，-6）．
由（1）题得：对称轴为x=1，顶点坐标为（1，-8），开口向上，故图象为：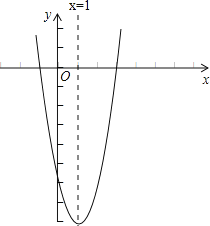

（3）当x=1时，y有最小值，最小值为-8，

∵，

∴y的最小值为10，

∴y的取值范围.

（4）当x=0时，y=-6；

当y=0时，2x2-4x-6=0,解得：x=3或x=-1,

函数图像与两坐标轴交点所围成的三角形的面积=.