题目内容
10. 如图,AB是⊙O的弦,∠OAB=20°,求弦AB所对的圆周角的度数.
如图,AB是⊙O的弦,∠OAB=20°,求弦AB所对的圆周角的度数.
分析 首先根据AO=BO,可得∠OBA=∠OAB=20°,然后根据三角形的内角和定理,判断出∠AOB=180°-20°-20°=140°,最后根据圆周角定理,判断出弦AB所对的圆周角是多少即可.
解答 解:∵AO=BO,
∴∠OBA=∠OAB=20°,
∴∠AOB=180°-20°-20°=140°,
∴弦AB所对的圆周角的度数是:140°÷2=70°;
∵弦AB所对的优弧的度数为:360°-140°=220°,
∴弦AB所对的圆周角的度数是:220°÷2=110°;
综上,可得
弦AB所对的圆周角的度数是70°或110°.
点评 (1)此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
(2)此题还考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.钟表的时针与分针在运行过程中每隔一定时间就相遇一次,相遇间隔的时间是( )
| A. | 1小时 | B. | $\frac{12}{11}$小时 | C. | 1.2小时 | D. | 1.1小时 |
5.下列运算正确的是( )
| A. | a•a3=a3 | B. | (ab)3=a3b | C. | (a3)2=a6 | D. | 2a2+a=3a3 |
15.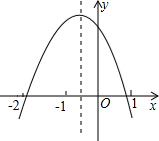 已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )| A. | abc>0 | B. | 2a-b<0 | C. | 4a-2b+c<0 | D. | (a+c)2>b2 |
2.一次函数y=kx+k(k<0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
19. 如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:
如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:
解答下列问题:
(1)表中的m=45,n=27.
(2)在扇形统计图中,“立定跳远”对应的圆心角的度数是72°.
(3)试估计全校1750名学生中参加“立定跳远”的人数.
 如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:
如图,某中学每个学期要求学生加强一项体育项目训练.为了解学生参加的项目情况,在全校1750名学生中,随机抽取了若干名学生进行调查,调查结果如表:| 项目名称 | 掷实心球 | 跳绳 | 50米短跑 | 立定跳远 | 仰卧起坐 | 健美操 |
| 人数 | 45 | 9 | m | 36 | n | 18 |
(1)表中的m=45,n=27.
(2)在扇形统计图中,“立定跳远”对应的圆心角的度数是72°.
(3)试估计全校1750名学生中参加“立定跳远”的人数.