题目内容
如图，BD是⊙O的直径，A、C是⊙O上的两点，且AB=AC，AD与BC的延长线交于点E.
（1）求证：△ABD∽△AEB；
（2）若AD=1，DE=3，求⊙O半径的长.
（1）证明：∵AB=AC， ∴弧AB=弧AC. ∴∠ABC=∠ADB.
又∠BAE=∠DAB，∴ △ABD∽△AEB.
（2）解：∵△ABD∽△AEB， ∴
.
∵ AD=1， DE=3， ∴AE=4. ∴ AB2=AD·AE=1×4=4.
∴ AB="2."
∵ BD是⊙O的直径， ∴∠DAB=90°.
在Rt△ABD中，BD2=AB2＋AD2=22＋12=5，
∴BD=
.∴⊙O的半径为
解析
练习册系列答案
相关题目
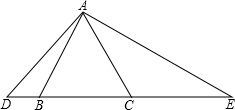如图，△ABC是一个边长为2的等边三角形，D、E都在直线BC上，并且∠DAE=120°
（2012•渝北区一模）如图，等边△ABC的边AB与正方形DEFG的边长均为2，且AB与DE在同一条直线上，开始时点B与点D重合，让△ABC沿这条直线向右平移，直到点B与点E重合为止，设BD的长为x，△ABC与正方形DEFG重叠部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
泰勒斯是古希腊哲学家，相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离．如图，B是观察点，船A在B的正前方，过B作AB的垂线，在垂线上截取任意长BD，C是BD的中点，观察者从点D沿垂直于BD的DE方向走，直到点E、船A和点C在一条直线上，那么△ABC≌△EDC，从而量出DE的距离即为船离岸的距离AB，这里判定△ABC≌△EDC的方法是（ ）
