题目内容
4.下列命题是真命题的有( )①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等;④若a2=b2,则a=b;⑤全等三角形的高相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据对顶角相等,平行线的性质,全等三角形的判定与性质,有理数的乘方对各小题分析判断即可得解.
解答 解:①对顶角相等,是真命题;
②两直线平行,内错角相等,是真命题;
③两个锐角对应相等的两个直角三角形全等,是假命题;
④若a2=b2,则a=b或a=-b,所以是假命题;
⑤应为全等三角形的对应高相等,所以,本命题是假命题;
综上所述,真命题有①②共2个.
故选B.
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.某中学举行校园歌手大赛,7位评委给选手小明的评分如下表:
若比赛的计分方法是:去掉一个最高分,去掉一个最低分,其余分数的平均值作为该选手的最后得分,则小明的最后得分为( )
| 评委 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 得分 | 9.8 | 9.5 | 9.7 | 9.8 | 9.4 | 9.5 | 9.4 |
| A. | 9.56 | B. | 9.57 | C. | 9.58 | D. | 9.59 |
9.如果$\sqrt{(2a-1)^{2}}$=2a-1,那么a的取值范围( )
| A. | a>$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
16.下列分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | m2+m-7=(m+3)(m-2)-1 | C. | (a+4)(a-4)=a2-16 | D. | x2-y2=(x+y)(x-y) |
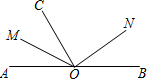 如图,O是直线AB上一点,OM平分∠AOC、ON平分∠BOC.
如图,O是直线AB上一点,OM平分∠AOC、ON平分∠BOC. 如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为点E,过点C作DA的平行线与AF相交于点F,CD=4$\sqrt{3}$,BE=2.
如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为点E,过点C作DA的平行线与AF相交于点F,CD=4$\sqrt{3}$,BE=2. 如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F. 如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )
如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )