题目内容
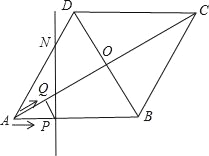
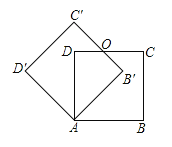
【题目】如图,将一长方形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 向终点
向终点![]() 运动,运动
运动,运动![]() 秒时,动点
秒时,动点![]() 从点
从点![]() 出发以相同的速度沿
出发以相同的速度沿![]() 向终点
向终点![]() 运动,当点
运动,当点![]() 、
、![]() 其中一点到达终点时,另一点也停止运动.
其中一点到达终点时,另一点也停止运动.
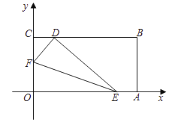
设点![]() 的运动时间为
的运动时间为![]() :(秒)
:(秒)
(1)![]() _________,
_________,![]() ___________(用含
___________(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,求点
处,求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的任意一点,过点
上的任意一点,过点![]() 作直线
作直线![]() 的平行线,与
的平行线,与![]() 轴交于
轴交于![]() 点,设直线
点,设直线![]() 的解析式为
的解析式为![]() ,当点
,当点![]() 与点
与点![]() 不重合时,设
不重合时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)6-t,t+![]() ;(2)D(1,3),y=
;(2)D(1,3),y=![]() x+
x+![]() ;(3)
;(3)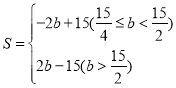
【解析】
(1)根据点E,F的运动轨迹和速度,即可得到答案;
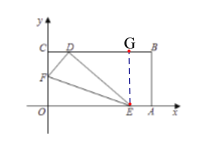
(2)由题意得:DF=OF=![]() ,DE=OE=5,过点E作EG⊥BC于点G,根据勾股定理得DG=4,进而得D(1,3),根据待定系数法,即可得到答案;
,DE=OE=5,过点E作EG⊥BC于点G,根据勾股定理得DG=4,进而得D(1,3),根据待定系数法,即可得到答案;
(3)根据题意得直线直线![]() 的解析式为:
的解析式为:![]() ,从而得M(
,从而得M(![]() ,3),分2种情况:①当点M在线段DB上时, ②当点M在DB的延长线上时,分别求出
,3),分2种情况:①当点M在线段DB上时, ②当点M在DB的延长线上时,分别求出![]() 与
与![]() 之间的函数关系式,即可.
之间的函数关系式,即可.
∵![]() ,
,![]() ,
,![]() ,
,
∴OA=6,OC=3,
∵AE=t×1= t,
∴![]() 6-t,
6-t,![]() (t+
(t+![]() )×1=t+
)×1=t+![]() ,
,
故答案是:6-t,t+![]() ;
;
(2)当![]() 时,
时,![]() 6-t=5,
6-t=5,![]() t+
t+![]() =
=![]() ,
,
∵将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,
处,
∴DF=OF=![]() ,DE=OE=5,
,DE=OE=5,
过点E作EG⊥BC于点G,则EG=OC=3,CG=OE=5,
∴DG=![]() ,
,
∴CD=CG-DG=5-4=1,
∴D(1,3),
设直线![]() 的解析式为:y=kx+b,
的解析式为:y=kx+b,
把D(1,3),E(5,0)代入y=kx+b,得![]() ,解得:
,解得: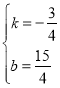 ,
,
∴直线![]() 的解析式为:y=
的解析式为:y=![]() x+
x+![]() ;
;
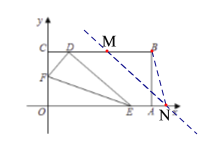
(3)∵MN∥DE,
∴直线直线![]() 的解析式为:
的解析式为:![]() ,
,
令y=3,代入![]() ,解得:x=
,解得:x=![]() ,
,
∴M(![]() ,3).
,3).
①当点M在线段DB上时,BM=6-(![]() )=
)=![]() ,
,
∴![]() =
=![]() ,
,
②当点M在DB的延长线上时,BM=![]() -6=
-6=![]() ,
,
∴![]() =
=![]() ,
,
综上所述: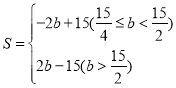 .
.

 名校课堂系列答案
名校课堂系列答案