题目内容
20. 某校为了举办全校运动会选拔了六名同学作为护旗手,已知护旗手站位如图所示,分别位于图中的点A、B、C、D、E、F处.假设护旗手的站位是随机安排的.
某校为了举办全校运动会选拔了六名同学作为护旗手,已知护旗手站位如图所示,分别位于图中的点A、B、C、D、E、F处.假设护旗手的站位是随机安排的.(1)甲同学是护旗手六人小组中的一员,求甲同学被分在四边形ABCD顶点处的概率;
(2)乙同学和丙同学都是此次护旗手小组的成员,求乙同学和丙同学的站位正好在四边形ABCD中同一条对角线的两个端点处的概率.
分析 (1)直接根据概率公式求解;
(2)先画树状图展示所有30种等可能的结果数,再找出乙同学和丙同学的站位正好在四边形ABCD中同一条对角线的两个端点处的结果数,然后根据概率公式求解.
解答 解:(1)甲同学被分在四边形ABCD顶点处的概率=$\frac{4}{6}$=$\frac{2}{3}$;
(2)画树状图如下:
共有30种等可能的结果数,其中乙同学和丙同学的站位正好在四边形ABCD中同一条对角线的两个端点处的结果数为4,
所以乙同学和丙同学的站位正好在四边形ABCD中同一条对角线的两个端点处的概率=$\frac{4}{30}$=$\frac{2}{15}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
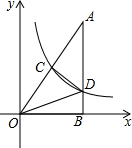 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)与斜边OA交于点C,与另一直角边交于点D,若OC:CA=1:2,且S△OCD=8,求k的值.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)与斜边OA交于点C,与另一直角边交于点D,若OC:CA=1:2,且S△OCD=8,求k的值. 如图,?ABCD中,E、F分别是边AB、CD的中点.
如图,?ABCD中,E、F分别是边AB、CD的中点. 在平行四边形ABCD中,E在DC上,若DE:EC=1:2,△FEC的面积是2,平行四边形ABCD的面积是13.
在平行四边形ABCD中,E在DC上,若DE:EC=1:2,△FEC的面积是2,平行四边形ABCD的面积是13. 如图,在?ABCD中,M,N分别是AD,BC的中点,连结AN,BM交于点P,连结CM,DN相交于点Q,则图中与△APM面积相等的三角形有几个?请一一列出,并说明理由.
如图,在?ABCD中,M,N分别是AD,BC的中点,连结AN,BM交于点P,连结CM,DN相交于点Q,则图中与△APM面积相等的三角形有几个?请一一列出,并说明理由.