题目内容
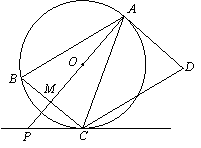
如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C与圆O相切的直线于点P。
(1)判断ÐBCP与ÐACD的数量关系,并说明理由。
(2)若AB=9,BC=6,求PC的长。
 |
(1) ÐBCP=ÐACD,
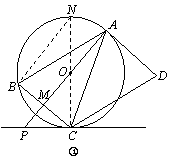
理由:如图j,连接CO并延长,交圆O于点N,连接BN。 ∵AB//CD,∴ÐBAC=ÐACD。
∵CN是圆O的直径,∴ÐCBN=90°。∴ÐBNC+ÐBCN=90°,
 ∵直线PC与圆O相切∴ÐPCO=90°,∴ÐBCP+ÐBCN=90°。
∵直线PC与圆O相切∴ÐPCO=90°,∴ÐBCP+ÐBCN=90°。
∴ÐBNC=ÐBCP。
又∵ÐBAC=ÐBNC,ÐBAC=ÐACD, 即ÐBCP=ÐACD
(2)∵AD是圆O的切线,∴AD^OA,即ÐOAD=90°。
∵BC//AD,∴ÐOMC=180°-ÐOAD=90°,即OM^BC。
∴MC=MB。∴AB=AC。
在Rt△AMC中,ÐAMC=90°,AC=AB=9,MC= 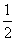 BC=3,
BC=3,
由勾股定理,得AM=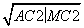 =
=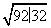 =6
=6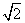 。
。
设圆O的半径为r。在Rt△OMC中,ÐOMC=90°,OM=AM-AO=6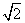 -r,MC=3,OC=r,
-r,MC=3,OC=r,
由勾股定理,得OM 2+MC 2=OC 2,即(6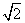 -r)2+32=r2。解得r=
-r)2+32=r2。解得r= 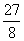
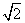 。
。
在△OMC和△OCP中, ∵ÐOMC=ÐOCP,ÐMOC=ÐCOP,
∴△OMC~△OCP。 ∴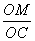 =
= 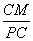 ,即
,即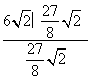 =
= 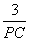 。
。
∴PC= 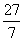 。
。

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 为
为 边上一点,且
边上一点,且 .
. ;
; 平分
平分 ,
, ,求
,求 的度数.
的度数.
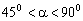 ,那么
,那么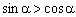 ;③若关于
;③若关于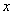 的方程
的方程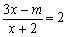 的解是负数,则m的取值范围为m<-4;④相等的圆周角所对的弧相等;⑤对于反比例函数
的解是负数,则m的取值范围为m<-4;④相等的圆周角所对的弧相等;⑤对于反比例函数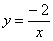 ,当
,当 B.
B.
 D.
D.
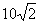 B.
B.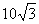 C.16 D. 20
C.16 D. 20