题目内容
16.(1)根据下列叙述填依据:已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°
所以AB∥EF(同旁内角互补,两直线平行 )
因为AB∥CD(已知 )
所以CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也平行 )
所以∠CDF+∠DFE=180°(两直线平行,同旁内角互补 )
所以∠B+∠BFD+∠D=∠B+∠BFE+∠EFD+∠D=360°
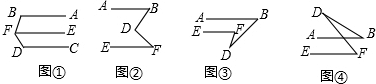
(2)根据以上解答进行探索,如图②,AB∥EF,∠BDF与∠B、∠F有何数量关系
(3)你能探索处图③、图④两个图形中,∠BDF与∠B、∠F的数量关系吗?请写出来.
分析 (1)根据平行线的性质和判定填空即可;
(2)过点D作AB的平行线DC,根据两直线平行,内错角相等证明即可;
(3)与(2)的证明方法类似,可以求出∠BDF与∠B、∠F的数量关系.
解答 解:因为∠B+∠BFE=180°,
所以AB∥EF(同旁内角互补,两直线平行 ),
因为AB∥CD(已知),
所以CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也平行),
所以∠CDF+∠DFE=180°(两直线平行,同旁内角互补),
所以∠B+∠BFD+∠D=∠B+∠BFE+∠EFD+∠D=360°;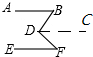 (2)过点D作AB的平行线DC,
(2)过点D作AB的平行线DC,
因为AB∥EF,
所以∠B=∠BDC,
因为AB∥EF,
所以CD∥EF,
所以∠F=∠FDC,
所以∠BDF=∠B+∠F
(3)过点D作AB的平行线DC,
根据平行线的性质可以证明图③∠BDF+∠B=∠F;图④∠BDF+∠B=∠F.
点评 本题考查的是平行线的性质和判定,正确作出辅助线是解题的关键.解答本题时,注意类比思想的运用.

练习册系列答案
相关题目
6.若不等式组$\left\{\begin{array}{l}x+7<3x+9\\ x>n\end{array}$的解集是x>4,则n的取值范围是( )
| A. | n≥4 | B. | n≤4 | C. | n=4 | D. | n<4 |
1.下列分数中,可以化为有限小数的是( )
| A. | $\frac{1}{15}$ | B. | $\frac{1}{18}$ | C. | $\frac{3}{15}$ | D. | $\frac{3}{18}$ |
