题目内容
如图,在平面直角坐标系xOy中,点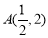 ,
,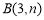 在反比例函数
在反比例函数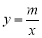 (m为常数)的图象G上,连接AO并延长与图象G的另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象G上,连接AO并延长与图象G的另一个交点为点C,过点A的直线l与x轴的交点为点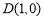 ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
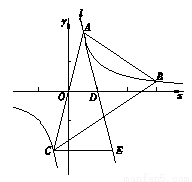
(1)求m的值及直线l对应的函数表达式;
(2)求点E的坐标;
(3)求证:∠BAE=∠ACB.
(1) ,
, ;(2)
;(2) ;(3)证明见试题解析.
;(3)证明见试题解析.
【解析】
试题分析:(1)∵ 点A在反比例函数 (m为常数)的图象G上,可得到m的值.设直线l对应的函数表达式为
(m为常数)的图象G上,可得到m的值.设直线l对应的函数表达式为 (k,b为常数,k≠0).由 直线l经过点
(k,b为常数,k≠0).由 直线l经过点 ,
, ,可求得直线l对应的函数表达式;
,可求得直线l对应的函数表达式;
(2)由反比例函数图象的中心对称性可知点C的坐标为 ,由 CE∥x轴交直线l于点E,得到点E的坐标为
,由 CE∥x轴交直线l于点E,得到点E的坐标为 ;
;
(3)如图,作AF⊥CE于点F,与过点B的y轴的垂线交于点G,BG交AE于点M,作CH⊥BG 于点H,则BH∥CE,∠BCE=∠CBH,先求出点F的坐标,得到 CF=EF,AC=AE,故有∠ACE =∠AEC.由于点 在图象G上,故可得B、G、H的坐标.在Rt△ABG中,求出tan∠ABH,在Rt△BCH中,求出tan∠CBH,可以得到∠ABH=∠CBH,∠BCE=∠ABH,从而有∠BAE=∠ACB.
在图象G上,故可得B、G、H的坐标.在Rt△ABG中,求出tan∠ABH,在Rt△BCH中,求出tan∠CBH,可以得到∠ABH=∠CBH,∠BCE=∠ABH,从而有∠BAE=∠ACB.
试题解析:【解析】
(1)∵ 点 在反比例函数
在反比例函数 (m为常数)的图象G上,∴
(m为常数)的图象G上,∴  .
.
∴ 反比例函数 (m为常数)对应的函数表达式是
(m为常数)对应的函数表达式是 .
.
设直线l对应的函数表达式为 (k,b为常数,k≠0).∵ 直线l经过点
(k,b为常数,k≠0).∵ 直线l经过点 ,
, ,∴
,∴  ,解得
,解得 ,∴ 直线l对应的函数表达式为
,∴ 直线l对应的函数表达式为 ;
;
(2)由反比例函数图象的中心对称性可知点C的坐标为 ,∵ CE∥x轴交直线l于点E,∴
,∵ CE∥x轴交直线l于点E,∴  ,∴ 点E的坐标为
,∴ 点E的坐标为 ;
;
(3)如图,作AF⊥CE于点F,与过点B的y轴的垂线交于点G,BG交AE于点M,作CH⊥BG 于点H,则BH∥CE,∠BCE=∠CBH,

∵  ,
, ,
, ,∴ 点F的坐标为
,∴ 点F的坐标为 ,∴ CF=EF,∴ AC=AE,∴ ∠ACE =∠AEC.∵ 点
,∴ CF=EF,∴ AC=AE,∴ ∠ACE =∠AEC.∵ 点 在图象G上,∴
在图象G上,∴  ,∴
,∴  ,
, ,
, .在Rt△ABG中,tan∠ABH=
.在Rt△ABG中,tan∠ABH= ,在Rt△BCH中,tan∠CBH=
,在Rt△BCH中,tan∠CBH= ,∴∠ABH=∠CBH,∴∠BCE=∠ABH,∵∠BAE=∠AMH-∠ABH=∠AEC-∠ABH,∠ACB=∠ACE-∠BCE,∴∠BAE=∠ACB.
,∴∠ABH=∠CBH,∴∠BCE=∠ABH,∵∠BAE=∠AMH-∠ABH=∠AEC-∠ABH,∠ACB=∠ACE-∠BCE,∴∠BAE=∠ACB.
考点:反比例函数综合题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 (
( )与一次函数
)与一次函数 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C,若△OAC的面积为1,且tan∠AOC=2.
轴于点C,若△OAC的面积为1,且tan∠AOC=2.
 的值小于一次函数
的值小于一次函数 的值.
的值.
 B.
B.


 的顶点坐标是( )
的顶点坐标是( ) 的图象与x轴只有一个公共点,求实数a的值.
的图象与x轴只有一个公共点,求实数a的值.
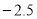 、
、 、2、
、2、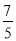 、
、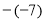 、0、-
、0、- 负有理数有 ( )
负有理数有 ( )