题目内容
19.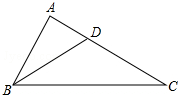 已知:如图,△ABC中,∠ABC=2∠C,BD平分∠ABC.
已知:如图,△ABC中,∠ABC=2∠C,BD平分∠ABC.(1)求证:BD=CD;
(2)试说明AB•BC=AC•CD.
分析 (1)根据∠ABC=2∠C,BD平分∠ABC可以求出∠ABD=∠DBC=∠C,然后证明出BD=CD;
(2)证得△ABD与△ACB相似,在根据相似三角形的对应边成比例列式整理即可得证.
解答 (1)证明:∵∠ABC=2∠C,BD平分∠ABC,
∴∠ABD=∠DBC=∠C,
∴BD=CD;
(2)解:在△ABD和△ACB中,
$\left\{\begin{array}{l}{∠A=∠A}\\{∠ABD=∠C}\end{array}\right.$,
∴△ABD∽△ACB,
∴$\frac{AB}{AC}$=$\frac{BD}{BC}$,
即AB•BC=AC•BD,
∴AB•BC=AC•CD.
点评 此题主要考查了相似三角形的判定与性质,角平分线的定义,等角对等边的性质,掌握三角形判定方法是解决问题的关键.

练习册系列答案
相关题目
4. 如图,△ABC为等边三角形,以AB为边向△ABC外侧作△ABD,使得∠ADB=120°,再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE,则下列结论:
如图,△ABC为等边三角形,以AB为边向△ABC外侧作△ABD,使得∠ADB=120°,再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE,则下列结论:
①D、A、E三点共线;②△CDE为等边三角形;③DC平分∠BDA;④DC=DB+DA,其中正确的有( )
 如图,△ABC为等边三角形,以AB为边向△ABC外侧作△ABD,使得∠ADB=120°,再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE,则下列结论:
如图,△ABC为等边三角形,以AB为边向△ABC外侧作△ABD,使得∠ADB=120°,再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE,则下列结论:①D、A、E三点共线;②△CDE为等边三角形;③DC平分∠BDA;④DC=DB+DA,其中正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.若X=2$\sqrt{2}$+$\sqrt{20}$,Y=3$\sqrt{3}$+$\sqrt{7}$,Z=$\sqrt{6}$+2$\sqrt{7}$,则( )
| A. | X最小 | B. | Y最小 | C. | Z最小 | D. | X、Y、Z一样大 |
 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为2.
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为2.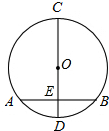 如图,在⊙O中,直径CD垂直于弦AB于点E.
如图,在⊙O中,直径CD垂直于弦AB于点E.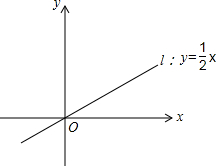 如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.
如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.