题目内容
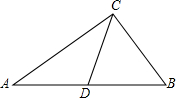
 如图,已知:Rt△ABC中,∠B=90°,AB=BC=2
如图,已知:Rt△ABC中,∠B=90°,AB=BC=2| 2 |
分析:此题可作DE⊥AC于E,在Rt△ADE中,通过求得AD及DE的长即可确定sin∠DAC.
解答: 解:过D作DE⊥AC于E;
解:过D作DE⊥AC于E;
在Rt△ABC中,
∵∠B=90°,AB=BC=2
,
∴∠C=45°.
∵点D为BC的中点,
∴BD=DC=
BC=
.
∴AD=
=
=
.
在Rt△DCE中,DE=DC•sin45°=1,
∴sin∠DAC=
.
 解:过D作DE⊥AC于E;
解:过D作DE⊥AC于E;在Rt△ABC中,
∵∠B=90°,AB=BC=2
| 2 |
∴∠C=45°.
∵点D为BC的中点,
∴BD=DC=
| 1 |
| 2 |
| 2 |
∴AD=
| AB2+BD2 |
(2
|
| 10 |
在Rt△DCE中,DE=DC•sin45°=1,
∴sin∠DAC=
| ||
| 10 |
点评:本题考查了解直角三角形的应用,关键是正确作出辅助线进行求解,比较简单.

练习册系列答案
相关题目
 如图:已知在Rt△ABC中,∠ACB=90°,CD是边AB上的中线,AC=6,cos∠ACD=
如图:已知在Rt△ABC中,∠ACB=90°,CD是边AB上的中线,AC=6,cos∠ACD= 23、如图,已知以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,
23、如图,已知以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE, 如图,已知在Rt△ABC中,AB=AC,以AB为直径作⊙O交BC于点F,连结OC交⊙O于点D,连结BD并延长交AC于点E,连结DF.
如图,已知在Rt△ABC中,AB=AC,以AB为直径作⊙O交BC于点F,连结OC交⊙O于点D,连结BD并延长交AC于点E,连结DF.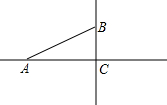 如图:已知在Rt△ABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为
如图:已知在Rt△ABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为