题目内容
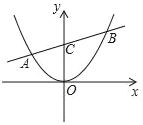
【题目】已知:如图直线y=![]() x+2与抛物线y=ax2交于A.B两点,点B的坐标(3,m),直线AB交y轴于点C.
x+2与抛物线y=ax2交于A.B两点,点B的坐标(3,m),直线AB交y轴于点C.
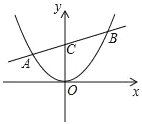

(1)求a,m的值;
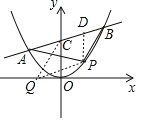
(2)点P在对称轴右侧的抛物线上,设P点横坐标为t,△PAB的面积为s,求s与t的函数关系式;
(3)在(2)的条件下,在x轴上有一点Q,当以B.C.P.Q为顶点的四边形是平行四边形时,求点Q的坐标.
【答案】(1)a=![]() ,m=3;(2)S=﹣
,m=3;(2)S=﹣![]() t2+
t2+![]() t+5或S=
t+5或S=![]() t2﹣
t2﹣![]() t﹣5;(3)点Q的坐标为(
t﹣5;(3)点Q的坐标为(![]() ﹣3,0).
﹣3,0).
【解析】试题分析:(1)把B(3,m)分别代入![]() 与
与![]() ,根据待定系数法即可求得;
,根据待定系数法即可求得;
(2)联立方程求得![]() 的坐标,设
的坐标,设![]() 点横坐标为
点横坐标为![]() ,则
,则![]() 进而求得D的坐标,然后根据
进而求得D的坐标,然后根据![]() 求得即可;
求得即可;
(3)由![]() 的坐标,根据平行四边形的性质即可确定
的坐标,根据平行四边形的性质即可确定![]() 的坐标为1,代入抛物线解析式求得横坐标,进而即可求得
的坐标为1,代入抛物线解析式求得横坐标,进而即可求得![]() 的坐标.
的坐标.
试题解析:(1)∵直线![]() 经过B(3,m),
经过B(3,m),
![]() 解得:m=3,
解得:m=3,
∴B(3,3),
代入![]() 得
得![]()
![]()
(2)由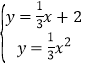 得
得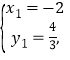
![]()
∴![]()
设P点横坐标为t,则![]()
把x=t代入![]() 得:
得:![]()
![]()
![]()
![]() 或
或![]()
(3)由直线AB为![]() 可知C(0,2),
可知C(0,2),
∵B(3,3),
∴B点的纵坐标和C点的差为32=1,
∴P、Q的纵坐标的差为1,
∵点Q在x轴上,
∴P的纵坐标为1,
代入抛物线![]() 得,
得,![]()
解得![]() 或
或![]() (舍去),
(舍去),
![]()
∵B的横坐标为3,
设Q(m,0),则![]()
![]()
∴点Q的坐标为![]()

练习册系列答案
相关题目