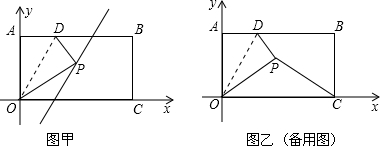
题目内容

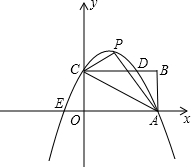
如图，矩形OABC的边OC，OA分别与x轴，y轴重合，点B的坐标是（ $数学公式$ ，1），点D是AB边上一个动点（与点A不重合），沿OD将△OAD翻折，点A落在点P处．
（1）若点P在一次函数y=2x-1的图象上，求点P的坐标；
（2）若点P在抛物线y=ax²图象上，并满足△PCB是等腰三角形，求该抛物线解析式；
（3）当线段OD与PC所在直线垂直时，在PC所在直线上作出一点M，使DM+BM最小，并求出这个最小值．

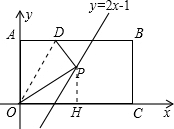解：（1）∵B（ $\text{[math]}$ ）
∴BC=OA=OP=1，OC= $\text{[math]}$ ．
∵点P在一次函数y=2x-1的图象上
∴设P（x，2x-1）
如图，过P作PH⊥x轴于H
在Rt△OPH中，PH=2x-1，OH=x，OP=1
∴x²+（2x-1）²=1
解得：x₁= $\text{[math]}$ ，x₂=0（不合题意，舍去）
∴P（ $\text{[math]}$ ， $\text{[math]}$ ）

（2）连接PB，PC

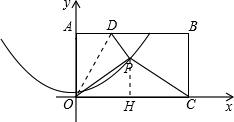①若PB=PC，则P在BC中垂线y= $\text{[math]}$ 上
∴设P（x， $\text{[math]}$ ），如图，过P作PH⊥x轴于H
在Rt△OPH中，PH= $\text{[math]}$ ，OH=x，OP=1
∴x²+ $\text{[math]}$ =1
解得：x₁= $\text{[math]}$ ，x₂=- $\text{[math]}$ （不合题意，舍去）
∴P（ $\text{[math]}$ ， $\text{[math]}$ ）
∴ $\text{[math]}$ =a× $\text{[math]}$ ，
得a= $\text{[math]}$
∴y= $\text{[math]}$ x²
②若BP=BC，则BP=1，连接OB
∵OP=1
∴OP+PB=2
∵在Rt△OBC中，∠OCB=90°，OB= $\text{[math]}$ =2
∴OP+PB=OB
∴O，P，B三点共线，P为线段OB中点．
又∵B（ $\text{[math]}$ ，1）
∴P（ $\text{[math]}$ ， $\text{[math]}$ ）
∴ $\text{[math]}$ =a× $\text{[math]}$ ，
解得：a= $\text{[math]}$
∴y= $\text{[math]}$ x²
③若CP=CB，则CP=1
∵OP=1
∴PO=PC，则P在OC中垂线x= $\text{[math]}$ 上
∴设P（ $\text{[math]}$ ，y）．
过P作PH⊥x轴于H，在Rt△OPH中，PH=|y|，OH= $\text{[math]}$ ，OP=1
∴y²+ $\text{[math]}$ =1
解得：y₁= $\text{[math]}$ ，y₂=- $\text{[math]}$
∴P（ $\text{[math]}$ ， $\text{[math]}$ ）或（ $\text{[math]}$ ，- $\text{[math]}$ ）
当点P（ $\text{[math]}$ ，- $\text{[math]}$ ）时，∠AOP=120°，此时∠AOD=60°，点D与点B重合，符合题意．
若点P（ $\text{[math]}$ ， $\text{[math]}$ ），则 $\text{[math]}$ =a× $\text{[math]}$ ，解得：a= $\text{[math]}$ ．∴y= $\text{[math]}$ x²
若点P（ $\text{[math]}$ ，- $\text{[math]}$ ），则- $\text{[math]}$ =a× $\text{[math]}$ ，解得：a=- $\text{[math]}$
∴y=- $\text{[math]}$ x²

（3）如图，∵△OAD沿OD翻折，点A落在点P处

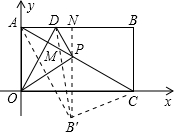∴OD垂直平分AP
∵PC⊥OD
∴A，P，C三点共线．
在Rt△AOD中，∠OAD=90°，OA=1
又可得：∠AOD=30°
∴AD=AO•tan30°= $\text{[math]}$ ，
∴D（ $\text{[math]}$ ，1）
作点B关于直线AC的对称点B′，过点B′作B′N⊥AB于点N，连接DB′，DB′与AC交点为M，此点为所求点．
∵∠ACB′=∠ACB=60°，∠ACO=30°
∴∠B′CO=30°
∵B′C=BC=1
∴B′（ $\text{[math]}$ ，- $\text{[math]}$ ），
∴N（ $\text{[math]}$ ，1）
在Rt△B′ND中，∠B′ND=90°，B′N= $\text{[math]}$ ，DN=AN-AD= $\text{[math]}$ - $\text{[math]}$ = $\text{[math]}$
∴DB′= $\text{[math]}$ = $\text{[math]}$
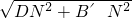∴DM+BM的最小值为 $\text{[math]}$ ．
分析：（1）先根据B（ $\text{[math]}$ ），可知BC=OA=OP=1，OC= $\text{[math]}$ ．设P（x，2x-1），过P作PH⊥x轴于H．利用x分别表示出PH、OH、又OP=1，根据勾股定理即可解答；
（2）连接PB，PC．①若PB=PC，设P（x， $\text{[math]}$ ），过P作PH⊥x轴于H．
在Rt△OPH中根据勾股定理解得x，从而确定P点坐标，进而求出解析式．
②若BP=BC，则BP=1，连接OB．在Rt△OBC中根据勾股定理求出OB，从而得出P为线段OB中点，求出P点坐标，进而求解析式．
③若CP=CB，则CP=1，PO=PC，则P在OC中垂线x= $\text{[math]}$ 上．设P（ $\text{[math]}$ ，y）．过P作PH⊥x轴于H．在Rt△OPH中根据勾股定理求出P点坐标，从而确定解析式．
（3）根据求最小值的解法，找对称点，构建直角三角形，利用勾股定理解答即可．
点评：本题考查二次函数的综合应用，其中涉及到的知识点有待定系数法求函数解析式和轴对称中的最小值问题，函数图象上点的意义，等腰三角形的性质等．要熟练掌握才能灵活运用．