Question

【题目】综合探究：

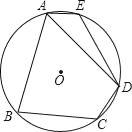
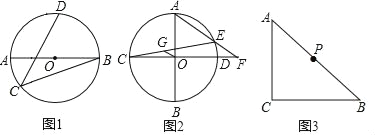
（1）如图1，AB是⊙O的直径，点C、D在上， ．若AB＝13，BC＝12，直接写出CD的长；

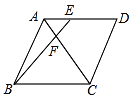
（2）如图2，AB、CD是⊙O的两条互相垂直的直径，E是劣弧AD上一点，AE的延长线交CD的延长线于F，过O作OG∥AE交CE于G，求AE：CG的值；

（3）如图3，∠ACB＝90°，AC＝BC，点P为AB的中点．若点E满足AE＝AC，CE＝CA，点Q为AE的中点，则＝　 　．

Answer 1

【答案】（1）CD＝；（2）；（3）．

【解析】

(1) 连接AC、BD，可得AD＝BD，再利用E、A、C三点共线，勾股定理即可解答.

(2) 作OH⊥OG，交CE于H，连接AH，证明△COG≌△AOH即可解答.

(3) 分点E在直线AC的左侧和右侧两种情况进行讨论， 利用勾股定理即可解答.

解：（1）如图1，连接AC、BD，

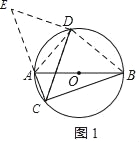
∵AB是⊙O的直径，

∴∠ADB＝∠ACB＝90°，

∵＝，

∴AD＝BD，

将△BCD绕点D，逆时针旋转90°到△AED处，

∴∠EAD＝∠DBC，

∵∠DBC+∠DAC＝180°，

∴∠EAD+∠DAC＝180°，

∴E、A、C三点共线，

∵AB＝13，BC＝12，

∴由勾股定理可求得：AC＝5，

∵BC＝AE，

∴CE＝AE+AC＝17，

∵∠EDA＝∠CDB，

∴∠EDA+∠ADC＝∠CDB+∠ADC，即∠EDC＝∠ADB＝90°，

∵CD＝ED，

∴△EDC是等腰直角三角形，

∴CE＝CD，

∴CD＝；

（2）作OH⊥OG，交CE于H，连接AH，

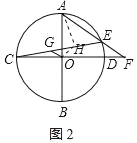
∵OG∥AE，

∴∠OGH＝∠AEC＝45°，

∴∠OHG＝45°，

∴OG＝OH，

又∵∠COG＝∠AOH＝90°﹣∠AOG，OC＝OA，

∴△COG≌△AOH（SAS），

∴CG＝AH，∠AHO＝∠CGO＝135°，

∴∠AHC＝90°，

∴AE＝AH＝CG，

∴＝．

（3）如图3，当点E在直线AC的左侧时，连接CQ，PC，

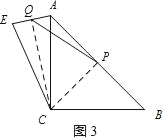
∵AC＝BC，∠ACB＝90°，

点P是AB的中点，

∴AP＝CP，∠APC＝90°，

又∵CA＝CE，点Q是AE的中点，

∴∠CQA＝90°，

设AC＝a，

∵AE＝AC，

∴AE＝a，

∴AQ＝AE＝a，

由勾股定理可求得：CQ＝a，

∵AQ+CQ＝PQ，

∴PQ＝a+a，

∴PQ＝AC，即＝；

如图4，当点E在直线AC的右侧时，连接CQ、CP，

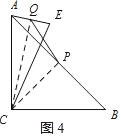
同理可知：∠AQC＝∠APC＝90°，

设AC＝a，

∴AQ＝AE＝a，

由勾股定理可求得：CQ＝a，

又PQ＝（CQ﹣AQ），

∴PQ＝AC，即＝；

综上，＝，

故答案为：．