题目内容
 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.(1)求证:AC平分∠DAB;
(2)若点E为
 |
| AB |
| 32 |
| 5 |
考点:切线的性质,勾股定理,等腰直角三角形,相似三角形的判定与性质
专题:几何综合题
分析:(1)首先连接OC,由直线CD与⊙O相切于点C,AD⊥CD,易证得OC∥AD,继而可得AC平分∠DAB;
(2)首先连接BC,OE,过点A作AF⊥CE于点F,可证得△ADC∽△ACB,△ACB∽△AFE,△ACF是等腰直角三角形,然后由相似三角形的对应边成比例以及勾股定理,即可求得答案.
(2)首先连接BC,OE,过点A作AF⊥CE于点F,可证得△ADC∽△ACB,△ACB∽△AFE,△ACF是等腰直角三角形,然后由相似三角形的对应边成比例以及勾股定理,即可求得答案.
解答:(1)证明:连接OC,
∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
即AC平分∠DAB;

(2)连接BC,OE,过点A作AF⊥EC于点F,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
=
,
即
=
,
解得:AB=10,
∴BC=
=6,
∵点E为
的中点,
∴∠AOE=90°,
∴OE=OA=
AB=5,
∴AE=
=5
,
∵∠AEF=∠B(同弧所对圆周角相等),∠AFE=∠ACB=90°,
∴△ACB∽△AFE,
∴
=
=
,
∴
=
=
,
∴AF=4
,EF=3
,
∵∠ACF=
∠AOE=45°,
∴△ACF是等腰直角三角形,
∴CF=AF=4
,
∴CE=CF+EF=7
.
∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
即AC平分∠DAB;

(2)连接BC,OE,过点A作AF⊥EC于点F,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
| AD |
| AC |
| AC |
| AB |
即
| ||
| 8 |
| 8 |
| AB |
解得:AB=10,
∴BC=
| AB2-AC2 |
∵点E为
 |
| AB |
∴∠AOE=90°,
∴OE=OA=
| 1 |
| 2 |
∴AE=
| OA2+OE2 |
| 2 |
∵∠AEF=∠B(同弧所对圆周角相等),∠AFE=∠ACB=90°,
∴△ACB∽△AFE,
∴
| AB |
| AE |
| AC |
| AF |
| BC |
| EF |
∴
| 10 | ||
5
|
| 8 |
| AF |
| 6 |
| EF |
∴AF=4
| 2 |
| 2 |
∵∠ACF=
| 1 |
| 2 |
∴△ACF是等腰直角三角形,
∴CF=AF=4
| 2 |
∴CE=CF+EF=7
| 2 |
点评:此题考查了切线的性质、相似三角形的判定与性质、勾股定理以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
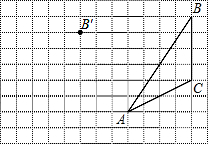 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 如图,在扇形OAB中,∠AOB=90°,点C是
如图,在扇形OAB中,∠AOB=90°,点C是 如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为
如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为