Question

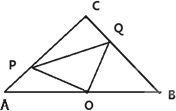
如下图，PQ为Rt△MPN斜边上的高， ∠M=45°，则图中等腰三角形的个数是

1. A.
   1个
2. B.
   2个
3. C.
   3个
4. D.
   4个

Answer 1

C
试题分析：由Rt△MPN， ∠M=45°，可得∠N=45°，由PQ为Rt△MPN斜边上的高，可得∠MPQ=∠N PQ= 45°，即可求得结果。
∵Rt△MPN中， ∠M=45°，
∴∠N=45°，
∵PQ为Rt△MPN斜边上的高，
∴∠MPQ=∠N PQ= 45°，
∵∠M=∠N，∠M=∠MPQ，∠N=∠NPQ，
∴△MPN、△MPQ、△NPQ是等腰三角形，
故选C.
考点：本题考查的是等腰三角形的判定，三角形的内角和定理
点评：解答本题的关键是掌握三角形的内角和为180°，等角对等边的性质。