题目内容
设各边均不相等三角形各边之长都是整数,周长小于13,那么这种三角形的个数共有( )A.1个
B.2个
C.3个
D.4个
【答案】分析:首先根据三角形的两边之和大于第三边以及三角形的周长,得到三角形的三边都不能大于5;
再结合三角形的两边之差小于第三边进行分析出所有符合条件的整数.
解答:解:根据三角形的两边之和大于第三边以及三角形的周长小于13,则其中的任何一边不能超过5;
再根据两边之差小于第三边,则这样的三角形共有3,4,2;4,5,2;3,4,5三个.
故选C.
点评:本题属竞赛题型,且涉及分类讨论的思想.解答的关键是找到三边的取值范围及对三角形三边的理解把握.
再结合三角形的两边之差小于第三边进行分析出所有符合条件的整数.
解答:解:根据三角形的两边之和大于第三边以及三角形的周长小于13,则其中的任何一边不能超过5;
再根据两边之差小于第三边,则这样的三角形共有3,4,2;4,5,2;3,4,5三个.
故选C.
点评:本题属竞赛题型,且涉及分类讨论的思想.解答的关键是找到三边的取值范围及对三角形三边的理解把握.

练习册系列答案
相关题目
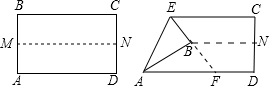
 8、如图,把矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕上,得到Rt△ABE,EB延长线交AD或AD的延长线于F,则△EAF是( )
8、如图,把矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕上,得到Rt△ABE,EB延长线交AD或AD的延长线于F,则△EAF是( )