Question

如图，把矩形ABCD纸对折，设折痕为MN，再把B点叠在折痕上，得到Rt△ABE，EB延长线交AD或AD的延长线于F，则△EAF是（　　）

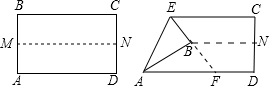
A．底边与腰不相等的等腰三角形；

B．各边均不相等的三角形；

C．或是各边不相等的三角形，或是底边与腰不相等的等腰三角形

D．等边三角形

Answer 1

如果将原来B点写作G点，AE和MN交于O，
∵M、N分别为AG、CD的中点，
∴EB=BF，又∠GEA=∠AEB
△EBA与△ABF中
∵AB=AB，BE=BF，AB⊥EF
∴△EBA≌△ABF
∴∠AEF=∠AFE
∵四边形ABCD为矩形，∴EC∥AD，
∴∠GEA=∠EAF，∠CEF=∠AFE=∠AEF=∠GEA
∴∠GEA+∠AEF+∠FEC=180°
∴∠AEF=60°
∴∠EAF=∠EFA=∠AEF=60°
因此△AEF是等边三角形．
故选D．