题目内容
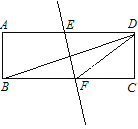 如图,将长方形纸片ABCD折叠,使点B与点D重合,折痕为EF,已知AB=6cm,BC=18cm,则Rt△CDF的面积是
如图,将长方形纸片ABCD折叠,使点B与点D重合,折痕为EF,已知AB=6cm,BC=18cm,则Rt△CDF的面积是
- A.27cm2
- B.24cm2
- C.22cm2
- D.20cm2
B
分析:求Rt△CDF的面积,CD边是直角边,有CD=AB=6cm,只要求出边FC即可.由于点B与点D重合,所以有FD=BF=BC-FC=18-FC,利用勾股定理可求出FC了.
解答:设FC=x,Rt△CDF中,CD=6cm,FC=x,又折痕为EF,
∴FD=BF=BC-FC=18-FC=18-x,
Rt△CDF中,DF2=FC2+CD2,
即(18-x)2=x2+62,
解得x=8,
∴面积为 ×FC×CD=
×FC×CD= ×8×6=24.
×8×6=24.
故选B.
点评:解决本题的关键是根据折叠及矩形的性质利用勾股定理求得CF的长度;易错点是得到DF与CF的长度和为18的关系.
分析:求Rt△CDF的面积,CD边是直角边,有CD=AB=6cm,只要求出边FC即可.由于点B与点D重合,所以有FD=BF=BC-FC=18-FC,利用勾股定理可求出FC了.
解答:设FC=x,Rt△CDF中,CD=6cm,FC=x,又折痕为EF,
∴FD=BF=BC-FC=18-FC=18-x,
Rt△CDF中,DF2=FC2+CD2,
即(18-x)2=x2+62,
解得x=8,
∴面积为
 ×FC×CD=
×FC×CD= ×8×6=24.
×8×6=24.故选B.
点评:解决本题的关键是根据折叠及矩形的性质利用勾股定理求得CF的长度;易错点是得到DF与CF的长度和为18的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 15、如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
15、如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( ) 19、如图,将长方形纸片的一角折叠,使顶点A落在A′处,EF为折痕,再将另一角折叠,使顶点B落在EA′上的B′点处,折痕为EG,则∠FEG等于
19、如图,将长方形纸片的一角折叠,使顶点A落在A′处,EF为折痕,再将另一角折叠,使顶点B落在EA′上的B′点处,折痕为EG,则∠FEG等于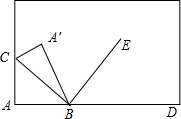 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的角平分线,求∠CBE的度数,并说明理由.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的角平分线,求∠CBE的度数,并说明理由. 如图,将长方形纸片的一角斜折,使顶点A落在A′处,EF为折痕;再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EG;观察并估计∠FEG=
如图,将长方形纸片的一角斜折,使顶点A落在A′处,EF为折痕;再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EG;观察并估计∠FEG= 如图,将长方形纸片ABCD沿对角线AC折叠,使点B落在点B′处,CB′交AD于点M.试说明△AMC的形状,并说明理由.
如图,将长方形纸片ABCD沿对角线AC折叠,使点B落在点B′处,CB′交AD于点M.试说明△AMC的形状,并说明理由.