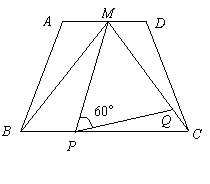
题目内容
如图13,在梯形![]() 中,
中,![]() 点
点![]() 是
是![]() 的中点,
的中点,![]() 是等边三角形.
是等边三角形.
(1)求证:梯形![]() 是等腰梯形;
是等腰梯形;
(2)动点![]() 、
、![]() 分别在线段
分别在线段![]() 和
和![]() 上运动,且
上运动,且![]() 保持不变.设
保持不变.设![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在(2)中:①当动点![]() 、
、![]() 运动到何处时,以点
运动到何处时,以点![]() 、
、![]() 和点
和点![]() 、
、![]() 、
、![]() 、
、![]() 中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当![]() 取最小值时,判断
取最小值时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
 |
(1)证明:∵![]() 是等边三角形
是等边三角形
∴![]()
∵![]() 是
是![]() 中点
中点
∴![]()
∵![]()
∴![]()
![]()
∴![]()
∴![]()
∴梯形![]() 是等腰梯形.
是等腰梯形.
 |
(2)解:在等边![]() 中,
中,![]()
![]()
![]()
∴![]()
∴![]()
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
(3)解:①当![]() 时,则有
时,则有![]()
则四边形![]() 和四边形
和四边形![]() 均为平行四边形
均为平行四边形
∴![]()
当![]() 时,则有
时,则有![]()
则四边形![]() 和四边形
和四边形![]() 均为平行四边形
均为平行四边形
∴![]()
∴当![]() 或
或![]() 时,以P、M和A、B、C、 D中的两个点为顶点的四边形是平行四边形.
时,以P、M和A、B、C、 D中的两个点为顶点的四边形是平行四边形.
此时平行四边形有4个.
②![]() 为直角三角形
为直角三角形
∵![]()
∴当![]() 取最小值时,
取最小值时,![]()
∴![]() 是
是![]() 的中点,
的中点,![]() 而
而![]()
∴![]() ∴
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,CE是梯形OABD的中位线,B点在函数y=
如图,CE是梯形OABD的中位线,B点在函数y=| k |
| x |
| A、1 | B、4 | C、8 | D、12 |
 (2012•嘉定区二模)如图,已知梯形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.
(2012•嘉定区二模)如图,已知梯形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC. 中,AB∥CD,AB=13,CD=4,点
中,AB∥CD,AB=13,CD=4,点 在边AB上,DE∥
在边AB上,DE∥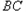 。
。
 ,且
,且 ,求
,求 的面积;
的面积;