题目内容
8.已知有9张卡片,分别写有1到9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则使关于x的不等式组$\left\{\begin{array}{l}4x≥3({x+1})\\ 3x<2a-1\end{array}\right.$有解的概率为( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解答 解:因为关于x的不等式组$\left\{\begin{array}{l}4x≥3({x+1})\\ 3x<2a-1\end{array}\right.$有解,
可得:$\left\{\begin{array}{l}{x≥3}\\{x<\frac{2a-1}{3}}\end{array}\right.$,
所以得出a>5,
因为a取≤9的整数,
可得a的可能值为6,7,8,9,共4种可能性,
所以使关于x的不等式组$\left\{\begin{array}{l}4x≥3({x+1})\\ 3x<2a-1\end{array}\right.$有解的概率为$\frac{4}{9}$;
故选C.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18.下列各数中最大的有理数是( )
| A. | $\frac{1}{3}$ | B. | -1 | C. | 0 | D. | $\sqrt{3}$ |
19.用代入法解方程组$\left\{\begin{array}{l}{2x-1=y}\\{3x-2y=1}\end{array}\right.$时,下列代入变形正确的是( )
| A. | 3x-4x-1=1 | B. | 3x-4x+1=1 | C. | 3x-4x-2=-1 | D. | 3x-4x+2=1 |
16.下列命题中,假命题是( )
| A. | 直角三角形的两个锐角互余 | B. | 三角形的外角和等于360° | ||
| C. | 两直线平行,同位角相等 | D. | 三角形的最大内角小于60° |
3.解分式方程$\frac{2}{x-1}$+$\frac{x+2}{1-x}$=1时,去分母变形后正确的是( )
| A. | 2-(x+2)=1 | B. | 2-x+2=x-1 | C. | 2-(x+2)=x-1 | D. | 2+(x+2)=x-1 |
13.在下列四个图案中是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.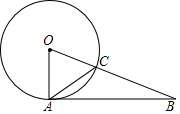 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )| A. | 20° | B. | 30° | C. | 50° | D. | 60° |